- 20 Tháng mười 2018
- 18
- 2
- 6
- Đồng Nai
- THPT Đoàn Kết
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
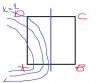
Tong thí nghiệm giao thoa trên mặt nước cho 2 nguồn A,B cách nhau 40cm có pt uA=uB=10cos(2pit). Tốc độ truyền sóng là 5cm/s. Xét hình vuông ABCD. Giả sử AD thay đổi được. Hãy tìm khoảng cách AD khi D thuộc cực đại trong 2 TH:
+ D xa A nhất
+ D gần A nhất
+ D xa A nhất
+ D gần A nhất