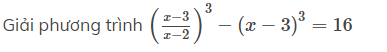Giải phương trình sau: ( x-3/x-2)^3 -(x-3)^3 =16
KhanhHuyen2006ĐKXĐ [imath]x \ne 2[/imath]
Đặt [imath]x-2=a \ne 0[/imath] , phương trình viết lại thành:
[imath]\left(1 -\dfrac{1}{a} \right)^3 - (a-1)^3 =16[/imath]
[imath]\iff 1 - \dfrac{3}{a} + \dfrac{3}{a^2} - \dfrac{1}{a^3} - a^3 + 3a^2 - 3a +1 = 16[/imath]
[imath]\iff a^3 + \dfrac{1}{a^3} - 3(a^2 + \dfrac{1}{a^2}) + 3(a+\dfrac{1}{a}) + 14 = 0[/imath]
Đặt [imath]\dfrac{1}{a} + a = y \Rightarrow a^2 + \dfrac{1}{a^2} = y^2 - 2 ; a^3 + \dfrac{1}{a^3} = y^3 - 3y[/imath]
Phương trình trở thành: [imath]y^3 -3y - 3y^2 + 6 + 3y +14 = 0[/imath]
[imath]\Leftrightarrow y^3 - 3y^2 + 20 = 0[/imath]
[imath]\Leftrightarrow (y+2)(y^2-5y+10) =0[/imath]
[imath]\Leftrightarrow y=-2 \Leftrightarrow a=-1 \Rightarrow x=1[/imath] (thỏa mãn)
Vậy phương trình có nghiệm duy nhất [imath]x=1[/imath]
Ngoài ra bạn tham khảo thêm kiến thức tại Phân tích đa thức thành nhân tử
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
