[imath]3\tan(x-\dfrac{\pi}{6})=\tan x[/imath]
ĐK: [imath]\begin{cases} x-\dfrac{\pi}{6} \ne \dfrac{\pi}{2}+k\pi\\ x\ \ne \dfrac{\pi}{2}+k\pi \end{cases}[/imath]
[imath]\begin{cases} x \ne \dfrac{2\pi}{3}+k\pi \\ x \ne \dfrac{\pi}{2}+k\pi \end{cases}[/imath]
Áp dụng công thức:
[imath]\tan(x-y)=\dfrac{\tan x -\tan y}{1+\tan x \tan y},[/imath],[imath]x-y\ne \dfrac{\pi}{2}+k\pi[/imath]
Khi đó phương trình tương đương:
[imath]3\dfrac{\tan x -\tan(\dfrac{\pi}{6})}{1+\tan x \tan(\dfrac{\pi}{6}}=\tan x[/imath]
[imath]\Leftrightarrow \dfrac{3\tan x -\sqrt{3}}{1+\tan x \dfrac{\sqrt{3}}{3}}=\tan x[/imath]
Đặt [imath]t=\tan x[/imath] ([imath]t \in \mathbb{R}[/imath])
Khi đó phương trình trở thành:
[imath]\dfrac{3t-\sqrt{3}}{1+\dfrac{\sqrt{3}}{3}t}=t[/imath] ([imath]t \ne -\sqrt{3}[/imath] vì 1+[imath]\tan x \dfrac{\sqrt{3}}{3} \ne 0[/imath] thế [imath]t=tanx[/imath] vào và giải sẽ ra điều kiện nhé )
[imath]\Leftrightarrow 3t-\sqrt{3}=t+\dfrac{\sqrt{3}}{3}t^2[/imath]
[imath]\Leftrightarrow \sqrt{3}t^2+6t-3\sqrt{3}=0[/imath]
[imath]\Leftrightarrow t=\sqrt{3}[/imath] (nhận)
Từ đó ta có: [imath]\tan x=\sqrt{3}[/imath]
hay [imath]\tan x=\tan(\dfrac{\pi}{3})[/imath]
[imath]\Leftrightarrow x=\dfrac{\pi}{3}+k\pi, k \in \mathbb{Z}[/imath]
Ta biểu diễn các vị trí của [imath]x[/imath] trên đường tròn lượng giác mà:
[imath]\begin{cases} x = \dfrac{2\pi}{3}+k\pi \\ x = \dfrac{\pi}{2}+k\pi \end{cases}[/imath]
Ta có thể dùng định lí:
Góc $x=\alpha+\dfrac{k2\pi}{n}$ ($n$ nguyên dương) sẽ có $n$ điểm biểu diễn vị trí của nó trên đường tròn lượng giác
Chỉ cần cho $k$ chạy từ $0$ đến $n-1$ sẽ tìm được $n$ điểm biểu diễn đó là: (mỗi điểm biểu diễn luôn có dạng $x=\beta+k2\pi$
$x_0=\alpha+\dfrac{0.2\pi}{n}+k2\pi$
$x_1=\alpha+\dfrac{1.2\pi}{n}+k2\pi$
....
$x_{n-1}=\alpha+\dfrac{(n-1)2\pi}{n}+k2\pi$
(ngoài ra có thể cho [imath]k[/imath] chạy trong 1 đoạn khác miễn là có [imath]n[/imath] phần tử VD: [imath]k=1,2,3,4,...,n[/imath] hoặc [imath]k=-1,0,1,2,....n-2[/imath]) nhưng hay chọn là [imath]k=0,1,2,3,...,n-1[/imath] như trên
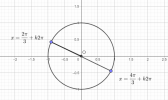
Ví dụ: [imath]x=\dfrac{2\pi}{3}+k\pi=\dfrac{2\pi}{3}+\dfrac{k2\pi}{2}[/imath] sẽ có 2 điểm biểu diễn vị trí của nó trên đường tròn lượng giác đó là:
[imath]x=\dfrac{2\pi}{3}+\dfrac{0.2\pi}{2}+k2\pi=\dfrac{2\pi}{3}+k2\pi[/imath]
[imath]x=\dfrac{2\pi}{3}+\dfrac{1.2\pi}{2}+k2\pi=\dfrac{5\pi}{3}+k2\pi[/imath]
(Có thể thế [imath]k[/imath] vào [imath]\dfrac{2\pi}{3}+k\pi[/imath] cho nhanh rồi cộng thêm [imath]k2\pi[/imath])
Hình:
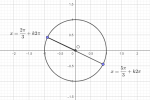
(Vẽ góc [imath]x=\beta+k2\pi[/imath] chỉ cần vẽ góc [imath]\beta[/imath] là được rồi)
Đó la 2 điểm biểu diễn góc [imath]x= \dfrac{2\pi}{3}+k\pi[/imath]
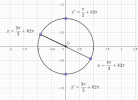
Tương tự ta vẽ cho góc
[imath]x' = \dfrac{\pi}{2}+k\pi[/imath] (nên đặt tên khác cho dễ phân biệt)
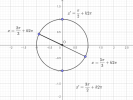
Nếu các vị trí biểu diễn nào của nghiệm [imath]x=\dfrac{\pi}{3}+k\pi[/imath] trùng với 1 trong 4 điểm trên hình trên thì ta sẽ bỏ chúng (lí do đơn giản là điều kiện không lấy 2 nghiệm
[imath]x= \dfrac{2\pi}{3}+k\pi[/imath] và [imath]x' = \dfrac{\pi}{2}+k\pi[/imath] nên ta cũng không lấy điểm biểu diễn của chúng từ đó ta bỏ các vị trí trùng với 1 trong 4 điểm trong hình trên)
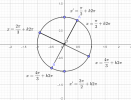
Biểu diễn nghiệm [imath]x=\dfrac{\pi}{3}+k\pi[/imath] ta được:
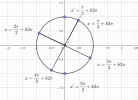
Các vị trí (điểm) biểu diễn nghiệm [imath]x=\dfrac{\pi}{3}+k\pi[/imath] là 2 điểm [imath]A,B[/imath] trên hình ,ta thấy chúng không trùng với 1 trong 4 điểm còn lại nên ta nhận nghiệm
[math]x=\dfrac{\pi}{3}+k\pi,k\in\mathbb{Z}[/math]
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
