 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Cực trị hàm trùng phương là một vấn đề quen thuộc trong các đề thi. Người ra đề có thể “bịa” rất nhiều câu hỏi khác nhau về vấn đề này. Ở đây mình chỉ đề cập tới một số vấn đề hay gặp nhất. Mọi người đóng góp thêm để chủ đề đầy đủ hơn nhé.
1. Cơ sở lý thuyết:
Cho hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c$.
TXĐ: $D=\mathbb{R}$.
Ta có: $y'=4a{{x}^{3}}+2bx$.
$y'=0\Leftrightarrow \left[ \begin{align}
& x=0 \\
& {{x}^{2}}=-\frac{b}{2a} \\
\end{align} \right.$
2. Một số kết quả đáng nhớ.
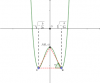
a, Đồ thị hàm số luôn có ít nhất một cực trị tại điểm $A\left( 0,c \right)$.
b, Điều kiện để hàm số có ba điểm cực trị: $-\frac{b}{2a}>0$ ($a,b$ trái dấu) (1) .
c, Khi hàm số thỏa mãn điều kiện (1), thì 3 điểm cực trị của hàm số tạo thành một tam giác cân ABC, cân tại $A\left( 0,c \right)$. Ta sẽ chứng minh được một số kết quả thú vị sau:
- $\tan \alpha =\frac{{{b}^{2}}}{4\left| a \right|}\sqrt{-\frac{2a}{b}}$ với $\alpha =\widehat{ABC}$.
- ${{S}_{\Delta ABC}}=\frac{{{b}^{2}}}{4\left| a \right|}\sqrt{-\frac{b}{2a}}$ .
- $R=\frac{{{b}^{3}}-8a}{8\left| a \right|b}$ với $R$ là bán kính đường tròn ngoại tiếp tam giác ABC.
(bạn đọc tự chứng minh các công thức trên nhé)
1. Cơ sở lý thuyết:
Cho hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c$.
TXĐ: $D=\mathbb{R}$.
Ta có: $y'=4a{{x}^{3}}+2bx$.
$y'=0\Leftrightarrow \left[ \begin{align}
& x=0 \\
& {{x}^{2}}=-\frac{b}{2a} \\
\end{align} \right.$
2. Một số kết quả đáng nhớ.

a, Đồ thị hàm số luôn có ít nhất một cực trị tại điểm $A\left( 0,c \right)$.
b, Điều kiện để hàm số có ba điểm cực trị: $-\frac{b}{2a}>0$ ($a,b$ trái dấu) (1) .
c, Khi hàm số thỏa mãn điều kiện (1), thì 3 điểm cực trị của hàm số tạo thành một tam giác cân ABC, cân tại $A\left( 0,c \right)$. Ta sẽ chứng minh được một số kết quả thú vị sau:
- $\tan \alpha =\frac{{{b}^{2}}}{4\left| a \right|}\sqrt{-\frac{2a}{b}}$ với $\alpha =\widehat{ABC}$.
- ${{S}_{\Delta ABC}}=\frac{{{b}^{2}}}{4\left| a \right|}\sqrt{-\frac{b}{2a}}$ .
- $R=\frac{{{b}^{3}}-8a}{8\left| a \right|b}$ với $R$ là bán kính đường tròn ngoại tiếp tam giác ABC.
(bạn đọc tự chứng minh các công thức trên nhé)
Last edited:

