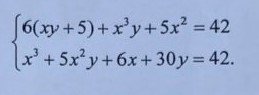Trừ vế theo vế 2 phương trình ta có:
[imath]x^3y -x^3 + 5x^2 - 5x^2 y + 6xy -6x + 30-30y =0[/imath]
[imath]\Leftrightarrow (y-1)(x^3 -5x^2 + 6x-30)=0[/imath]
[imath]\Leftrightarrow (y-1)(x-5)(x^2 +6) = 0[/imath]
TH1: [imath]y=1[/imath]
Thay vào pt 2 ta có:
[imath]x^3 +5x^2 + 6x+30 =42[/imath]
[imath]\Leftrightarrow x^3+5x^2 + 6x -12=0[/imath]
[imath]\Leftrightarrow (x-1)(x^2+6x+12)=0[/imath]
Mà [imath]x^2+6x+12= (x+3)^2 + 3 > 0[/imath]
[imath]\Leftrightarrow x=1[/imath]
TH2: [imath]x=5[/imath]
Thay vào phương trình 2 ta có:
[imath]125 + 125y + 30 + 30y =42[/imath]
[imath]\Leftrightarrow y = \dfrac{-113}{155}[/imath]
Vậy [imath](x,y) \in \{ (1;1) ; (5; \dfrac{-113}{155}) \}[/imath]
Ngoài ra mời bạn tham khảo:Tổng hợp kiến thức cơ bản toán 9
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
