- 26 Tháng mười một 2017
- 22
- 5
- 46
- 19
- TP Hồ Chí Minh
- Trường Trung học Cơ sở Hoa Lư
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
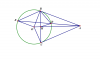
Cho đường tròn ( O; R) và điểm A nằm ngoài đường tròn. Hai tiếp tuyến AB, AC của ( O ) với B, C là tiếp điểm. Cát tuyến ADE với D,E thuộc (O), D nằm giữa A và E. Tia AD nằm giữa 2 tia AB VÀ AO. Gọi H là giao điểm của OA và BC. Chứng minh tứ giác DEOH nội tiếp.