 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Sau một hồi nghiên cứu khá rắc rối em đã giải được bài 1, nó khá dễ nhưng hơi rối xíu.Bài 1 nhờ mem sau giải nhé.
Bài 6. Có nhiều sách giải theo kiểu chọn tâm quay tức thời tại điểm nối vuông góc 2 vecto vận tốc tại A và B, nhưng cách này mình thấy cơ sở luận không vững chắc.
Mình đề xuất cách giải khác như sau:
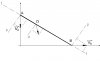
- Nguyên tắc: Có thể phân chuyển động của thanh thành 2 chuyển động tịnh tiến và quay quanh tâm. Vì là thanh cứng, nên vecto vận tốc quanh tâm tức thời (nằm trên thanh) phải tỷ lệ với khoảng cách đến tâm.View attachment 127570
- Cách giải:
Phân tích vecto vận tốc tại A, B và D thành 2 thành phần: dọc theo trục thanh gọi là Vt, vuông góc với trục thanh gọi là Vp.
- Vì thanh không biến dạng nên ta phải có V_At = V_Bt = V_Dt hay VB.cos30 = VA.cos60 Ta tính được VA cũng như V_Dt
Tính VA_p và V_Bp. 2 vecto vận tốc này chính là thành phần gây ra chuyển động quay quanh tâm tức thời nằm trên thanh.
Có VA_p và V_Bp ta tìm được vị trí tâm quay tức thời. Vị trí tâm quay sẽ phải đảm bảo tốc độ góc: w = V_Ap/R = V_Bp/(AB - R)
Ta tính được R là vị trí tâm quay tức thời O, sau đó tính khoảng cách OD ---> Tính được V_Dp = w.OD
Tính được vận tốc của điểm D khi đã có 2 thành phần vuông góc là V_Dt và V_Dp.
cho mik hỏi là u-v và u+v là vận tốc của cái nàoThế bài 1 a hiến thêm cách giải đỡ rắc rối hơn nhé.
Chiều dài sóng âm (tính từ dao động âm đầu tiên đế dao động âm cuối cùng) do tàu phát ra là:
L_s = to (u - v)
Sau khi bị phản hồi đến tàu, khoảng thời gian tiếp nhận sóng âm là:
t = L_s(u+v) => L_s = t(u+v)
Thay L_s vào trên, rút v ra là có kết quả thôi
Lúc đầu thì sóng âm và tàu ngầm cùng chiều nên vận tốc tương đối sẽ là u-v, lúc sau thì ngược chiều nên là u+vcho mik hỏi là u-v và u+v là vận tốc của cái nào
vậy là quãg đườg truyền và thu tín hiệu lại là như nhau ak bạnLúc đầu thì sóng âm và tàu ngầm cùng chiều nên vận tốc tương đối sẽ là u-v, lúc sau thì ngược chiều nên là u+v
Độ dài sóng phát ra và thu vào là như nhau nha bạn.vậy là quãg đườg truyền và thu tín hiệu lại là như nhau ak bạn

