Toán 9 Giải các bài toán liên quan đến đường tròn

[Mori Ran 680]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

ai biết những bài trên hình thì giúp mk với ạ, mk cảm ơn ạ

 

[TranPhuong27]

Bài 15:
a) Theo hệ thức lượng: [TEX]OH=\frac{OB^2}{OA} = \frac{3^2}{6} = \frac{3}{2}[/TEX]
b) Chu vi [TEX]AFE = AE+AF+FE=AE+AF+MF+ME=AE+AF+FC+BE = (AE+EB)+(AF+FC) = AB+AC=2AB=2 \sqrt{OA^2-OB^2}=6 \sqrt{3}[/TEX]
c) [TEX] \widehat{DOE}=\frac{1}{2} . ( \widehat{MOC}+\widehat{MOB})=\frac{1}{2} . \widehat{BOC}=\widehat{AOB}[/TEX]
Ta có: Ta có [TEX]cos \widehat{AOB}=\frac{OB}{OA} = \frac{1}{2} [/TEX]
=> [TEX]\widehat{AOB}=60^0[/TEX]
=> [TEX]\widehat{DOE}=60^0[/TEX]

Bài 16:
a) Gọi giao điểm của MN với (O) là K, giao điểm của AK với OM là P, ON với KM là Q
Ta có [TEX]\widehat{AKB}=90^0[/TEX] => AK vuông góc KB
Theo tính chất 2 tiếp tuyến thì AK vuông góc OM, BK vuông góc ON
Do đó OPKQ là HCN => [TEX]\widehat{MON}=90^0[/TEX]
b) Theo tính chất 2 tiếp tuyến cắt nhau: [TEX]AM=MK,BN=KN[/TEX]
=> [TEX]AM+NB=MK+KM=MN[/TEX]
c) [TEX]AM.BN=MK.KN=OK^2=R^2[/TEX]

 

[7 1 2 5]

11. Điều kiện [TEX]\widehat{MAB}=90^o[/TEX] sai nha bạn. Chắc là [TEX]\widehat{MAB}=60^o[/TEX]
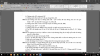
a) Ta thấy: [tex]\widehat{AMB}=\widehat{ANB}=90^o \Rightarrow AM \perp MB, AN \perp NB[/tex]
Dễ thấy AB là trung trực của MN nên BM = BN. Từ đó (B,BM) đi qua N. Mà [TEX]AM \perp MB, AN \perp NB[/TEX] nên AM, AN là 2 tiếp tuyến của đường tròn.
b) Ta có MN = 2MH.
Lại có: [tex]MH^2=AH.HB \Rightarrow MN^2=4MH^2=4AH.HB[/tex]
c) Ta có: [tex]\widehat{MAB}=60^o \Rightarrow \widehat{NBM}=60^o[/tex]. Mà BMN cân tại B nên BMN đều.
Lại có: O là tâm đường tròn ngoại tiếp của BMN, BMN đều nên O cũng là trọng tâm của BMN.
d) Ta thấy: ME là đường kính của (O) nên [TEX]\widehat{MNE}=90^o[/TEX]
MF là đường kính của (B) nên [TEX]\widehat{MNF}=90^o[/TEX]
Từ đó suy ra N,E,F thẳng hàng.