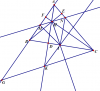
cho tam giác ABC (AB<AC) các đường cao AD BE CF cắt nhau tại H gọi I là trung điểm BC đường thẳng vg góc với HI tại H cắt AB AC thứ tự tại M N
a) CM góc AMH=góc CHI
b) AM.HI=MH.CH
c) tam giác IMN cân
______________________________________________________________________
a) Ta có: [tex]\widehat{CHI}+\widehat{CHN}=90 \Rightarrow \widehat{CHI}+\widehat{MHF}=90[/tex]
Mà: [tex]\widehat{MHF}+\widehat{AMH}=90\Rightarrow \widehat{AMH}=\widehat{CHI}[/tex]
b) Có: [tex]\widehat{MAH}=\widehat{ICH}[/tex] (Cung phụ [tex]\widehat{ABC}[/tex]
Mà có 2 góc $
\widehat{AMH}=\widehat{CHI} $
. Suy ra đồng dạng suy ra tỉ số
c) Qua $C$ kẻ đường thẳng song song với $MN$ cắt $AB$ tại $G$ và cắt $AD$ tại $K$
Dễ dàng chứng minh được: [tex]KI \bot CH[/tex]
Mà: [tex]AB \bot CH[/tex]
\Rightarrow [tex]KI \parallel AB[/tex] Hay [tex]KI \parallel BG[/tex]
Mà: $IB=IC$. Suy ra $KG=KC$
Mà: [tex]\frac{MH}{GK}=\frac{NH}{CK}(=\frac{AH}{AK})[/tex]
Suy ra: $HM=HN$
Xét tam giác [tex] IMN[/tex] có: $IH$ vừa là đường cao vừa là trung tuyến suy ra tam giác $IMN$ cân
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
