Toán 12 Giá trị của f(0).

[Tungtom]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Giúp em bài này với ạ, em cảm ơn mọi người.

 

[Kaito Kidㅤ]

Cách của mình nghĩ không biết có tối ưu không vì nó hơi dài , bạn cứ tham khảo thử nhé
Gọi hàm số đó là: [tex]f(x)=ax^3+bx^2+cx+d[/tex]
Do nó đi qua $A;B;C$ nên ta có hệ:
[tex]\left\{\begin{matrix} & a+b+c+d=1 (1)& \\ & 8a+4b+2c+d=4 (2)& \\ & 27a+9b+3c+d=9 (3)& \end{matrix}\right.[/tex]
Đường thẳng qua $AB;BC;CA$ có phương trình lần lượt : $y=3x-2; y=5x-6, y=4x-3$
Phương trình hoành độ của $f(x)$ với đường thẳng $AB$: $ax^3+bx^2+(c-3)x+d+2=0$
$x=1;x=2$ là 2 nghiệm của PT này, ta chia lược đồ Hoocne :

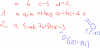
Vậy hoành độ của $M$ là: [tex]x_M=\frac{-3a-b}{a}[/tex]
Tương tự với 2 TH kia ta có: [tex]x_N=\frac{-4a-b}{a};x_P=\frac{-5a-b}{a}[/tex]
Theo đề: [tex]x_M+x_N+x_P=5\Leftrightarrow -17a-3b=0[/tex]
Vậy giải hệ [tex]\left\{\begin{matrix} & a+b+c+d=1 (1)& \\ & 8a+4b+2c+d=4 (2)& \\ & 27a+9b+3c+d=9 (3)& \\ &17a-3b=0 &\end{matrix}\right.[/tex]
Có:

Vậy $f(0)=d=-18$ chọn B

 

[Lê.T.Hà]

Nhìn tọa độ đặc biệt của 3 điểm A, B, C (đều thuộc [tex]y=x^2[/tex]) thì mình nghĩ tới ý tưởng [tex]y=f(x)[/tex] cắt [tex]y=x^2[/tex] tại 3 điểm A, B, C nên [tex]f(x)-x^2=a(x-1)(x-2)(x-3)\Rightarrow f(x)=x^2+a(x-1)(x-2)(x-3)[/tex]
Khi đó hoành độ M là nghiệm:
[tex]f(x)=3x-2\Leftrightarrow x^2-3x+2+a(x-1)(x-2)(x-3)=0\Leftrightarrow (x-1)(x-2)[1+a(x-3)]=0[/tex]
[tex]\Rightarrow x_M=\frac{3a-1}{a}[/tex]
Tương tự với N, P. Sau đó cộng lại được 5, dễ dàng tìm a
Mình nghĩ thế này khối lượng tính toán sẽ giảm đi 1 lượng khổng lồ

 

[iceghost]

Quan sát của bạn trên là hay rồi, nhưng có một cách để gọn hơn nữa:

Tổng hoành độ $x_M + x_N + x_P = (x_M + x_A + x_B) + (x_N + x_A + x_C) + (x_P + x_B + x_C) - 2(x_A + x_B + x_C)$

Ở đây các bộ hoành độ của $(M, A, B), (N, A, C), (P, B, C)$ là các nghiệm của pt với đường thẳng nên tổng các nghiệm của pt, theo định lý Vi-ét, chỉ phụ thuộc vào hệ số trước $x^2$ hay có giá trị bằng $-\dfrac{b}a$ (hoặc nếu tinh mắt hơn thì có thể thấy nó bằng ba lần hoành độ điểm uốn)

Thay số vào, tìm ra $\dfrac{b}a = -\dfrac{17}3$. Vậy là ta thu được pt còn lại của hệ pt đầu lời giải @KaitoKidaz