[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
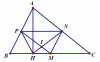
Cho tg $ABC$ có $AB<AC$ đg cao $AH$. Gọi $M,N,P$ là tđ của $BC, CA, AB$
a, Cm $MNPH$ là hthang cân
b, Giả sử $PM$ vg $NH$, Cm $PN+HM=AH$
Giúp em!
a, Cm $MNPH$ là hthang cân
b, Giả sử $PM$ vg $NH$, Cm $PN+HM=AH$
Giúp em!