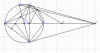
Cho đường tròn (O) đường kính BC, điểm A bất kì trên (O) sao cho AB>AC. Tiếp tuyến tại A của (O) cắt BC tại D, E đối xứng với A qua BC, EA cắt BC tại M. Kẻ đường cao AH của tam giác ABE, AH cắt BC tại F.
a. Chứng minh: AFEC là hình thoi
b. Chứng minh: [tex]DB.DC=DM.DO[/tex]
c. Gọi I là trung điểm AH, BI cắt (O) tại K.
Chứng minh: AIMK nội tiếp
d. AK cắt BD tại N. Chứng minh: N là trung điểm MD.
a) Xét $\Delta ABE$ có $BM$ và $AH$ là đường cao $\Rightarrow F $ là trực tâm
Ta có: $AF//EC$ (cùng vuông với BE); $AC//EF$ (cùng vuông với AB)
$CF; AE$ cắt nhau tại trung điểm mỗi đường
Suy ra $AFEC$ là hình thoi
b) Xét $\Delta ADC $ và $\Delta BDA$
có $\widehat{ADC}$ chung; $\widehat{CAD}=\widehat{ABC}$
Suy ra $\Delta ADC \sim \Delta BDA\Rightarrow \dfrac{AD}{DC}=\dfrac{BD}{DA}\Rightarrow DC.DB=AD^2$
Xét $\Delta AOD$ vuông tại $A$ có đường cao $AM$
$\Rightarrow AD^2= DM.DO$
Suy ra $DC.DB= DM.DO$
c) $MI$ là đường trung bình của $\Delta AHE$
$\Rightarrow MI//HE\Rightarrow \widehat{AEB}=\widehat{AMI}$
Mà $\widehat{AEB}=\widehat{AKB}$
Suy ra $\widehat{AKI}=\widehat{AMI}\Rightarrow AKMI$ nội tiếp
d) Ta có: $\widehat{AIM}=90^\circ\Rightarrow \widehat{AKM}=90^\circ$
Xét $\Delta AMN$ vuông tại $M$ có đường cao $MK$
$\Rightarrow MN^2=NK.NA$
Gọi $S$ là giao điểm của $DK$ và $(O)$
Ta có: $\widehat{KMD}=\widehat{MAN}=\widehat{KED}$
$\Rightarrow MKDE$ nội tiếp $\Rightarrow \widehat{EMD}=\widehat{EKD}=90^\circ$
$\Rightarrow SE$ là đường kính $(O)$
Ta có $SA//BD$ (cùng vuông với $AE$)
$\Rightarrow \widehat{ASK}=\widehat{SKD}$
Mà $\widehat{ASK}=\widehat{DAK}$
Suy ra $\widehat{DAK}=\widehat{KDN}$
Vậy $\Delta ADN\sim \Delta DKN\Rightarrow NK.NA=DN^2$
Suy ra $MN=ND$
Có gì khúc mắc em hỏi lại nhé
Ngoài ra em tham khảo thêm kiến thức tại đây nhé
https://diendan.hocmai.vn/threads/t...o-ban-hoan-toan-mien-phi.827998/#post-4045397
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
