 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Bài 4 bạn có thể giải kĩ hơn cho mình đc k mình kém phần đường tròn lắmCâu 1:
View attachment 73032
Xét [tex]\triangle OAE[/tex] và [tex]\triangle OBF[/tex] có:
OA=OB
OE=OF(gt)
[tex]\angle OEA=\angle OFB[/tex] ( cùng bù với [tex]\angle OEF=\angle OFE[/tex] )
=> [tex]\triangle OAE= \triangle OBF(c-g-c)\Rightarrow AE=BF[/tex]
Câu 4:
View attachment 73035
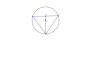
Dễ dàng chứng minh AH = HB = [tex]\frac{AB}{2}=\frac{R\sqrt{3}}{2}[/tex]
Áp dụng định lý Pi-ta-go cho tam giác AOH tính được OH = [tex]\frac{1}{2}R[/tex]
=> HC = OH+OC= [tex]\frac{3}{2}R[/tex]
Tiếp tục áp dụng định lý Pi-ta-go đối với 2 tam giác AHC và BHC, tính được AC = AB =[tex]R\sqrt{3}[/tex]=AB
=> đpcm
Câu 2, 3 mình nghĩ bạn chỉ cần thay số vào là làm được thôi.
Tam giác AOB (bạn tự nối vào nha) có OA= OB = R=> tam giác AOB cân tại A => AH = HB = [tex]\frac{AB}{2}=\frac{R\sqrt{3}}{2}[/tex]Bài 4 bạn có thể giải kĩ hơn cho mình đc k mình kém phần đường tròn lắm
Cảm ơn bạn nhé mà b2 và b3 cách lm kiểu j vậy mấy dạng này mình học k đc chắcTam giác AOB (bạn tự nối vào nha) có OA= OB = R=> tam giác AOB cân tại A => AH = HB = [tex]\frac{AB}{2}=\frac{R\sqrt{3}}{2}[/tex]
Áp dụng định lý Pi-ta-go cho tam giác AOH có:
[tex]OH^2=AO^2-AH^2=R^2-(\frac{R\sqrt{3}}{2})^2=\frac{1}{4}R^2=\frac{1}{2}R[/tex]
=>HC= OH+OC=[tex]\frac{1}{2}R+R=\frac{3}{2}R[/tex]
Áp dụng định lý Pi-ta-go đối với tam giác AHC có:[tex]AC^2=AH^2+HC^2=(\frac{R\sqrt{3}}{2})^2+(\frac{3}{2}R)^2=3R^2\Rightarrow AC=R\sqrt{3}[/tex]
Mà AH = HB, CH vuông góc AB nên tam giác ABC cân tại C => CB = AC = [tex]R\sqrt{3}[/tex] =AB
=> AB=AC=BC=> đpcm

ko có gì, nhưng lần sau nếu bạn muốn cảm ơn thì ko cần làm vậy đâu, có thể bị báo cáo đó, nhấn like là đủ rồiThank mình hiểu r , cảm ơn nh

