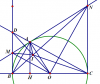
Cho nửa đg tròn tâm O đk BC Vẽ 2 tiếp tuyến Bx, Cy của (O). Gọi A là điểm trên nửa đg tròn sao cho AB<AC. Tiếp tuyến tại A của (O) cắt Bx,Cy tại M và N. Vẽ đ/c AH của tam giác ABC.Đường thẳng AC cắt Bx tại D. CM: OD vuông góc BN
_________________________________________________________________________
Dễ dàng chứng minh được: $OBMA;OCNA$ là tứ giác nội tiếp
Và: [tex]\widehat{MON}=90^{\circ}\Leftrightarrow \Delta MON[/tex] vuông (Bài toán thường làm)
Ta có: [tex]\widehat{BOM}=\widehat{MOA}(BOAMnt)[/tex]
Mà: [tex]\widehat{MOA}=\widehat{ANO}[/tex] (Cùng phụ với [tex]\widehat{AON}[/tex] )
[tex]\widehat{ANO}=\widehat{CNO}[/tex]
[tex]\Rightarrow \widehat{BOM}=\widehat{CNO}[/tex]
Xét: [tex]\Delta OMB;\Delta NOC[/tex] có:
[tex]\widehat{MBO}=\widehat{NCO}(=90^{\circ})[/tex]
[tex]\widehat{BOM}=\widehat{CNO}[/tex] (cmt)
[tex]\Rightarrow \Delta OMB \sim \Delta NOC(g.g)\Rightarrow \frac{MB}{OC}=\frac{BO}{NC}\Rightarrow \frac{2MB}{OB}=\frac{2BO}{NC}\Rightarrow \frac{BD}{OB}=\frac{BC}{NC}[/tex]
Mà: [tex]\widehat{DBO}=\widehat{BCN}(=90^{\circ})[/tex]
Suy ra: [tex]\Delta DBO\sim \Delta BCN(c.g.c)\Rightarrow \widehat{ODB}=\widehat{NBC}[/tex]
Mà: [tex]\widehat{NBC}+\widehat{DBI}=90^{\circ}\Rightarrow \widehat{DBI}+\widehat{ODB}=90^{\circ}\Rightarrow \widehat{BID}=90^{\circ}[/tex]
[tex]\Rightarrow OD\perp BN[/tex]
$P/S:$ Bài này giải hơi bị chi tiết!

 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.


