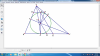
Vẽ đường kính DG, AG kéo dài cắt BC tại Q, K, J lần lượt là giao điểm của (I) với AC, AB
Tiếp tuyến tại G cắt AB, AC lần lượt tại H, O
Ta thấy IO là phân giác [tex]\widehat{GIK}[/tex], IC là phân giác $\widehat{DIK}$ (tính chất của tiếp tuyến nha)
=> IO vuông góc với IC
=> $IK^2 = OK.KC = OG.CD$
Tương tự với IJ => $IJ^2 = HG.BD$
=> OG.CD = HG.BD => $\frac{HG}{OG} = \frac{CD}{BD}$ (*)
Vì OH song song với BC => $\frac{OG}{CQ} = \frac{OA}{AC} = \frac{AH}{AB} = \frac{HG}{BQ}$
=> $\frac{HG}{OG} = \frac{BQ}{CQ}$ (**)
(*), (**) => $\frac{BQ}{CQ} = \frac{CD}{BD}$ => $\frac{BC}{CQ} = \frac{BC}{BD}$ => BD = CQ
Mà BM = CM => MD = MQ => M là trung điểm DQ
=> MN // AQ (Vì MN là đường trung bình)
Mà IN // AG (Vì IN là đường trung bình)
=>I, M, N thẳng hàng
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
