- 10 Tháng sáu 2017
- 660
- 794
- 131
- 22
- Phú Thọ
- THPT Thanh Thủy
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
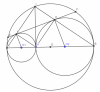
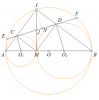
Trong mặt phẳng cho đoạn AB, điểm M là điểm di động giữa hai điểm A và B sao cho AM < BM. Vẽ hai đường tròn đường kính Am và BM có tâm lần lượt là có tâm O1 và O2 , tiếp tuyến chung ngoài của hai đường tròn tiếp xúc với ( O1) taijC, tiếp xúc với (O2) tại D. Gọi I là giao điểm của hai đường thẳng AC và BD.
a, Chứng minh tứ giác ABCD là tứ giác nội tiếp và IM là tiếp tuyến chung của hai đường tròn (O1) , (O2).
b,Chứng minh rằng [tex]DC^{2}[/tex] = IB.ID
c, Khi AM = 3cm, BM= 6cm. Đường tròn (O) đường kính AB, đường thẳng CD cắt (O) lần lượt tại E, F sao cho E nằm trên cũng nhỏ AF. Tính độ dài EF
@Blue Plus , @iceghost @quynhphamdq
Các bạn trình bày rõ giúp mình nha Mình cần câu c.
Mình cần câu c.
a, Chứng minh tứ giác ABCD là tứ giác nội tiếp và IM là tiếp tuyến chung của hai đường tròn (O1) , (O2).
b,Chứng minh rằng [tex]DC^{2}[/tex] = IB.ID
c, Khi AM = 3cm, BM= 6cm. Đường tròn (O) đường kính AB, đường thẳng CD cắt (O) lần lượt tại E, F sao cho E nằm trên cũng nhỏ AF. Tính độ dài EF
@Blue Plus , @iceghost @quynhphamdq
Các bạn trình bày rõ giúp mình nha
 Mình cần câu c.
Mình cần câu c.