[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
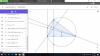
Cho tam giác ABC nhọn nội tiếp (O), 3 đường cao AD, BE, CF cắt nhau tại H
a. CMR AH=2OM với M là trung điểm BC
b. Gỉa sử BC cố định, A di động sao Góc BAC nhọn tìm vị trí A để Diện tích tam giác BHC lớn nhất
c. CMR $\sin ^2A+\sin ^2B+\sin ^2C>2$
d. Tìm vị trí của điểm A sao DH.DA lớn nhất
e. CMR $EF=AH\cdot \sin \widehat{BAC}$
j. CMR $\cos A\cdot \cos B+\cos B\cdot \cos C+\cos C\cdot \cos A=1$
g. CMR $\cos A+\cos B+\cos C\ge \sqrt{3}$
h. CMR $\cos A+\cos B+\cos C\le \frac{3}{2}$
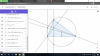
a. CMR AH=2OM với M là trung điểm BC
b. Gỉa sử BC cố định, A di động sao Góc BAC nhọn tìm vị trí A để Diện tích tam giác BHC lớn nhất
c. CMR $\sin ^2A+\sin ^2B+\sin ^2C>2$
d. Tìm vị trí của điểm A sao DH.DA lớn nhất
e. CMR $EF=AH\cdot \sin \widehat{BAC}$
j. CMR $\cos A\cdot \cos B+\cos B\cdot \cos C+\cos C\cdot \cos A=1$
g. CMR $\cos A+\cos B+\cos C\ge \sqrt{3}$
h. CMR $\cos A+\cos B+\cos C\le \frac{3}{2}$
