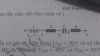[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
1, Một mạch điện xoay chiều ABDEF gồm các linh kiện sau đây mác nối tiếp ( hình vẽ)
- Một cuôn dây có hệ số tự cảm L và không có điện trở.
- Hai điện trở giống nhau, mỗi cái có giá trị R
- Một tụ có điện dung C