Vật A chuyển động tròn đều với bán kính quỹ đạo 8 cm và chu kì 0,2 s. Vật B có khối lượng 100 g dao động điều hoà theo phương thẳng đứng với biên độ 10 cm và tần số 5 Hz. Tâm I quỹ đạo tròn của vật A cao hơn vị trí cân bằng O của vật B là 1 cm (hình vẽ). Mốc tính thời gian lúc hai vật ở thấp nhất, lấy pi^2=10 . Khi hai vật ở ngang nhau lần thứ 5 kể từ thời điểm ban đầu thì lực đàn hồi của lò xo có độ lớn
View attachment 162813
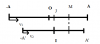
Vật A chuyển động tròn đều nên có thể xem là nó đang dao động điều hòa quanh điểm I với biên độ A'=R=8 (cm) và chu kì [tex]T_1=0,2(s)[/tex]
Theo đề ra ta có: [tex]T_2=\frac{1}{f}=0,2(s)=T_1=T[/tex]
[tex]\Rightarrow \omega =\frac{2\pi}{T}=10\pi (rad/s)\Rightarrow k=m\omega^2=0,1.100.10=100(N/m)[/tex]
[tex]\Rightarrow \Delta l_0=\frac{mg}{k}=0,01(m)=1(cm)[/tex]
[tex]\Rightarrow[/tex] Vị trí lò xo không biến dạng J ngang với I
Vì hai vật có cùng chu kì và I cao hơn O nên trong 1 chu kì hai vật ở ngang nhau 2 lần => 2 chu kì hai vật ngang nhau 4 lần
Gọi M là điểm mà tại đó hai vật ngang nhau lần thứ 5; [tex]\Delta t[/tex] là thời gian 2 vật di chuyển từ biên âm đến khi ngang nhau lần thứ 5.
Ta có phương trình giao động của vật 1 là:
[tex]x=10cos(10\pi t-\pi)[/tex]
Phương trình giao động của vật 2 là:
[tex]x=1+8cos(10\pi t-\pi)[/tex]
Sau khoảng thời gian [tex]\Delta t[/tex] vị trí của hai vật là:
[tex]x_A=10cos(10\pi.\Delta t-\pi)[/tex]
[tex]x_B=1+8cos(10\pi.\Delta t-\pi)[/tex]
2 vật ngang nhau nên: [tex]x_A=x_B\Leftrightarrow 10cos(10\pi.\Delta t-\pi)=1+8cos(10\pi.\Delta t-\pi)[/tex]
[tex]\Rightarrow \Delta t=\frac{2}{15}(s)=\frac{T}{2}+\frac{T}{6}[/tex]
[tex]\Rightarrow[/tex] OM=[tex]\frac{A_1}{2}=5(cm)[/tex] [tex]\Rightarrow \Delta l=JM=OM-OJ=5-1=4(cm)=0,04(m)[/tex]
[tex]\Rightarrow F=K.\Delta l=100.0,04=4(N)[/tex]
M ở trên J nên đây là lực nén => [tex]\vec{F}[/tex] hướng xuống
=> Chọn B
Bài này mình k chắc đoạn delta t :< ai đọc được soi lỗi với nha
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
