- 27 Tháng hai 2017
- 2,140
- 4,212
- 644
- 20
- Cần Thơ
- THPT Chuyên Lý Tự Trọng
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Như ta đã biết công thức tính cường độ điện trường tạo bởi một điện tích điểm là [imath]E=\frac{k.|q|}{\varepsilon r^{2}}[/imath]. Nhưng nếu xét một vật mang điện thì sao? Đặc biệt hơn là vật mang điện đó có hình dạng đặc biệt (hình cầu, mặt phẳng, hình trụ,...).
Ta có 2 phương pháp để giải quyết vấn đề này, đó là Phương pháp vi phân và Phương pháp áp dụng định lý O-G (Ostrogradski-Gauss). Hôm nay chúng ta sẽ đi tìm hiểu phương pháp áp dụng định lý O-G, bên cạnh đó sẽ có một số bài tập vận dụng để có thể hiểu rõ hơn về phương pháp này.
I. LÝ THUYẾT
1. Điện thông
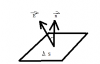
- Xét một diện tích S có vector pháp tuyến [imath]\vec{n}[/imath] nằm trong vùng điện trường đều [imath]\vec{E}[/imath]. Lúc đó, thông lượng điện trường đi qua diện tích S đó là một đại lượng vô hướng, được ký hiệu là [imath]\phi[/imath] và có giá trị bằng:
[tex]\phi =E.S.cos(\vec{E},\vec{n})[/tex]
- Nếu như diện tích S đó không phẳng và điện trường [imath]\vec{E}[/imath] không đều. Ta sẽ xét một diện tích [imath]\Delta S[/imath] đủ nhỏ để được xem là phẳng và tại đó điện trường $\vec{E} xem là đều:
[tex]\Delta \phi =E.\Delta S.cos(\vec{E},\vec{n})[/tex].
- [imath]\Delta \phi[/imath] có thể nhận giá trị âm dương tùy theo chiều pháp tuyến [imath]\vec{n}[/imath] mà ta chọn.
- Khi xét về độ lớn, điện thông ([imath]\Delta \phi[/imath]) qua mặt [imath]\Delta S[/imath] có ý nghĩa là số đường sức (N) đi qua mặt diện tích đó.
Tổng quát lại, nếu muốn xác định điện thông [imath]\phi[/imath] qua một mặt S bất kỳ, ta cũng sẽ chia mặt đó thành các nguyên tố diện tích [imath]\Delta S[/imath]. Điện thông mỗi mặt nhỏ đó sẽ là [imath]\Delta \phi[/imath]. Điện thông qua mặt S đó sẽ là:
*Lưu ý: Đối với mặt kín, khi tính điện thông ta luôn chọn chiều của pháp tuyến [imath]\vec{n}[/imath] là chiều hướng ra phía ngoài của mặt S nào đó.
2. Định lý O-G (Ostrogradski-Gauss)
a) Định lý O-G cho chân không. (Có phần chứng minh nhưng mình sẽ lược bớt mà chỉ nhấn vào trọng tâm phần định lý, bạn nào cần và cảm thấy khó hiểu thì mình sẽ chứng minh ở bài viết tiếp nhé )
- Định lý O-G cho chân không sẽ được phát biểu như sau: Điện thông qua một mặt kín có giá trị bằng tổng đại số các điện tích bên trong mặt đó chia cho hằng số điện [imath]\varepsilon _0[/imath]:
b) Định lý O-G cho môi trường điện môi.
- Nếu như trong môi trường điện môi thì ta sẽ có thêm hằng số điện môi [imath]\varepsilon[/imath] thôi và phát biểu cũng tương tự như Định lý O-G cho chân không vậy, lúc đó ta sẽ có công thức:
Ta có 2 phương pháp để giải quyết vấn đề này, đó là Phương pháp vi phân và Phương pháp áp dụng định lý O-G (Ostrogradski-Gauss). Hôm nay chúng ta sẽ đi tìm hiểu phương pháp áp dụng định lý O-G, bên cạnh đó sẽ có một số bài tập vận dụng để có thể hiểu rõ hơn về phương pháp này.
I. LÝ THUYẾT
1. Điện thông
- Xét một diện tích S có vector pháp tuyến [imath]\vec{n}[/imath] nằm trong vùng điện trường đều [imath]\vec{E}[/imath]. Lúc đó, thông lượng điện trường đi qua diện tích S đó là một đại lượng vô hướng, được ký hiệu là [imath]\phi[/imath] và có giá trị bằng:
[tex]\phi =E.S.cos(\vec{E},\vec{n})[/tex]
- Nếu như diện tích S đó không phẳng và điện trường [imath]\vec{E}[/imath] không đều. Ta sẽ xét một diện tích [imath]\Delta S[/imath] đủ nhỏ để được xem là phẳng và tại đó điện trường $\vec{E} xem là đều:
[tex]\Delta \phi =E.\Delta S.cos(\vec{E},\vec{n})[/tex].
- [imath]\Delta \phi[/imath] có thể nhận giá trị âm dương tùy theo chiều pháp tuyến [imath]\vec{n}[/imath] mà ta chọn.
- Khi xét về độ lớn, điện thông ([imath]\Delta \phi[/imath]) qua mặt [imath]\Delta S[/imath] có ý nghĩa là số đường sức (N) đi qua mặt diện tích đó.
Tổng quát lại, nếu muốn xác định điện thông [imath]\phi[/imath] qua một mặt S bất kỳ, ta cũng sẽ chia mặt đó thành các nguyên tố diện tích [imath]\Delta S[/imath]. Điện thông mỗi mặt nhỏ đó sẽ là [imath]\Delta \phi[/imath]. Điện thông qua mặt S đó sẽ là:
| [tex]\phi =\sum \Delta \phi =\sum E.\Delta Scos(\vec{E},\vec{n})[/tex] |
*Lưu ý: Đối với mặt kín, khi tính điện thông ta luôn chọn chiều của pháp tuyến [imath]\vec{n}[/imath] là chiều hướng ra phía ngoài của mặt S nào đó.
2. Định lý O-G (Ostrogradski-Gauss)
a) Định lý O-G cho chân không. (Có phần chứng minh nhưng mình sẽ lược bớt mà chỉ nhấn vào trọng tâm phần định lý, bạn nào cần và cảm thấy khó hiểu thì mình sẽ chứng minh ở bài viết tiếp nhé )
- Định lý O-G cho chân không sẽ được phát biểu như sau: Điện thông qua một mặt kín có giá trị bằng tổng đại số các điện tích bên trong mặt đó chia cho hằng số điện [imath]\varepsilon _0[/imath]:
| [tex]\phi = \frac{1}{\varepsilon _0}\sum_{i}q_i[/tex] |
b) Định lý O-G cho môi trường điện môi.
- Nếu như trong môi trường điện môi thì ta sẽ có thêm hằng số điện môi [imath]\varepsilon[/imath] thôi và phát biểu cũng tương tự như Định lý O-G cho chân không vậy, lúc đó ta sẽ có công thức:
| [tex]\phi = \frac{1}{\varepsilon \varepsilon _0}\sum_{i}q_i[/tex] |
Last edited: