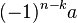[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Định lí Vi-ét thuận :
Nếu phương trình bậc hai có dạng : ax^2 + bx + c = 0 (a ≠ 0) có 2 nghiệm phân biệt x1, x2 thì
Định lí Vi-ét đảo :
Nếu ta có hai số u, v có u + v = S và u.v = P thì u và v là nghiệm của phương trình :
X^2 – SX + P = 0
Phương trình đa thức bất kì :
Cho phương trình:
Cho x1, x2,..., xn là n nghiệm của phương trình trên, thì:
Nhân toàn bộ vế phải ra, chúng ta sẽ có công thức Viète, được phát biểu như sau:
và trong hàng k bất kỳ, vế phải của đẳng thức là
còn vế trái được tính như sau:
- Nếu x1, x2, x3 là nghiệm của phương trình
thì công thức Viète (sau khi chia đều hai bên cho a3 tức a, và chuyển dấu trừ nếu có qua vế phải) cho ta:
Nếu phương trình bậc hai có dạng : ax^2 + bx + c = 0 (a ≠ 0) có 2 nghiệm phân biệt x1, x2 thì
Định lí Vi-ét đảo :
Nếu ta có hai số u, v có u + v = S và u.v = P thì u và v là nghiệm của phương trình :
X^2 – SX + P = 0
Phương trình đa thức bất kì :
Cho phương trình:
Cho x1, x2,..., xn là n nghiệm của phương trình trên, thì:
Nhân toàn bộ vế phải ra, chúng ta sẽ có công thức Viète, được phát biểu như sau:
và trong hàng k bất kỳ, vế phải của đẳng thức là
- Tổng của: các tích từng cụm (n-k) các nghiệm của phương trình trên.
- Nếu x1, x2, x3 là nghiệm của phương trình
thì công thức Viète (sau khi chia đều hai bên cho a3 tức a, và chuyển dấu trừ nếu có qua vế phải) cho ta:
