Toán 9 Diện tích tứ giác BEFC?

[nguyễn hồ bảo nguyên]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

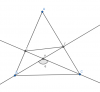
Cho tam giác ABC có 2 đường cao BF và CE cắt nhau tại H. Biết góc BHC = 119 độ 23 phút 57 giây và diện tích tam giác AEF = 6,7 cm2 . Tính diện tích tứ giác BEFC

 

[Tạ Đặng Vĩnh Phúc]

* Ta dễ dàng chứng minh tam giác AEF đồng dạng tam giác ACB (góc A chung, ngoài ra còn AFE = ABC, hệ quả do tứ giác EFCB nội tiếp)
* Như vậy dễ thấy $S_{AEF} = k^2 . S_{ABC}$
Vấn đề còn lại là đi tìm tỉ số đồng dạng k = $\frac{AE}{AC}$
Dễ thấy $\frac{AE}{AC} = cos A = cos (180^o - \widehat{EHF}) = cos (180^o - \alpha)$