Đề tự ôn hsg toán 9

[tthandb]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Bài 1:
a) Với x,y không âm, tìm giá trị nhỏ nhất của biểu thức:

b) Cho a; b; c > 0 và:

. Tìm giá trị lớn nhất của abc.
Bài 2:
Cho các số

, và x+y+z =12.
Tìm giá trị lớn nhất của biểu thức P = xyz
Bài 3: Cho a, b, c là số đo độ dài các cạnh của một tam giác thỏa a + b + c = 2. Chứng minh rằng

.
Bài 4: Cho a, b, c là các số dương. Chứng minh bất đẳng thức :

Bài 5: Cho 3 số a, b, c thỏa mãn

. Tìm giá trị lớn nhất của biểu thức :

Giúp giùm!!!​

 

[1um1nhemtho1]

Bài 3: Cho a, b, c là số đo độ dài các cạnh của một tam giác thỏa a + b + c = 2. Chứng minh rằng

.

Bài 3: ta có BĐT tam giác $a+b > c$ \Rightarrow $2c < a+b+c = 2$ \Rightarrow $c < 1$
tương tự cũng có $a<1$ và $b<1$

\Rightarrow $(a-1)(b-1)(c-1) < 0$
\Leftrightarrow $abc -(ab+bc+ac) +(a+b+c) - 1 < 0$ $(1)$

có $ab+bc+ac = \frac{(a+b+c)^2-(a^2+b^2+c^2)}{2}= \frac{4-(a^2+b^2+c^2)}{2} $
\Rightarrow $(1)$ \Leftrightarrow $abc -\frac{4-(a^2+b^2+c^2)}{2} +2 - 1 < 0$
\Leftrightarrow $a^2+b^2+c^2 + 2abc < 2$

 

[1um1nhemtho1]

Bài 1:

b) Cho a; b; c > 0 và:

. Tìm giá trị lớn nhất của abc.

$\frac{1}{1+a}+\frac{1}{1+b}+\frac{1}{1+c}=2$
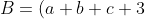\Leftrightarrow $\frac{1}{1+a}= (1-\frac{1}{1+b})+(1-\frac{1}{1+c})$
\Leftrightarrow $ \frac{1}{1+a}=\frac{b}{1+b}+\frac{c}{1+c}$

Áp dụng BĐT Cauchy có:

$\frac{b}{1+b}+\frac{c}{1+c} \ge \frac{2\sqrt{bc}}{\sqrt{(1+b)(1+c)}}$
\Leftrightarrow $\frac{1}{1+a} \ge \frac{2\sqrt{bc}}{\sqrt{(1+b)(1+c)}}$ (1)

tương tự có: $\frac{1}{1+b} \ge \frac{2\sqrt{ac}}{\sqrt{(1+a)(1+c)}}$ (2)
và $\frac{1}{1+c} \ge \frac{2\sqrt{ab}}{\sqrt{(1+a)(1+b)}}$ (3)

nhân (1) và (2) và (3) vế theo vế suy ra

$abc \le \frac{1}{8}$

\Rightarrow $max_{abc}=\frac{1}{8}$

xảy ra khi $a=b=c=\frac{1}{2}$