[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Giúp mình bài hình của đề này với ạ
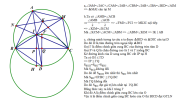
Câu [imath]4(3,5[/imath] điểm). Cho [imath](O; \mathrm{R})[/imath] và dây cung [imath]\mathrm{BC}[/imath] cố định không đi qua [imath]\mathrm{O}[/imath]. Điểm [imath]\mathrm{A}[/imath] di chuyến trên cung lớn [imath]\mathrm{BC}(\mathrm{A}[/imath] khác [imath]\mathrm{B}, \mathrm{C})[/imath]. Vẽ đường phân giác góc [imath]\mathrm{B}[/imath] và góc [imath]\mathrm{C}[/imath] của tam giác [imath]\triangle \mathrm{A} B C[/imath] cắt nhau tại [imath]I[/imath] và cắt [imath](O)[/imath] lần lượt tại [imath]\mathrm{M}[/imath] và [imath]\mathrm{N}[/imath]. Tia [imath]\mathrm{Al}[/imath] cắt [imath](O)[/imath] tại [imath]\mathrm{D}[/imath].
a) Chứng minh [imath]\Delta M A I[/imath] cân.
b) Gọi giao điểm của [imath]\mathrm{AC}[/imath] và [imath]\mathrm{MN}[/imath] là [imath]\mathrm{K}[/imath]. chứng minh [imath]IK[/imath] song song với [imath]\mathrm{AB}[/imath].
c) Khi điểm [imath]\mathrm{A}[/imath] di chuyển trên cung lớn [imath]\mathrm{AB}[/imath], tìm vị trí của điểm [imath]\mathrm{A}[/imath] để diện tích tứ giác [imath]B I C D[/imath] đạt giá trị lớn nhất.
Câu [imath]4(3,5[/imath] điểm). Cho [imath](O; \mathrm{R})[/imath] và dây cung [imath]\mathrm{BC}[/imath] cố định không đi qua [imath]\mathrm{O}[/imath]. Điểm [imath]\mathrm{A}[/imath] di chuyến trên cung lớn [imath]\mathrm{BC}(\mathrm{A}[/imath] khác [imath]\mathrm{B}, \mathrm{C})[/imath]. Vẽ đường phân giác góc [imath]\mathrm{B}[/imath] và góc [imath]\mathrm{C}[/imath] của tam giác [imath]\triangle \mathrm{A} B C[/imath] cắt nhau tại [imath]I[/imath] và cắt [imath](O)[/imath] lần lượt tại [imath]\mathrm{M}[/imath] và [imath]\mathrm{N}[/imath]. Tia [imath]\mathrm{Al}[/imath] cắt [imath](O)[/imath] tại [imath]\mathrm{D}[/imath].
a) Chứng minh [imath]\Delta M A I[/imath] cân.
b) Gọi giao điểm của [imath]\mathrm{AC}[/imath] và [imath]\mathrm{MN}[/imath] là [imath]\mathrm{K}[/imath]. chứng minh [imath]IK[/imath] song song với [imath]\mathrm{AB}[/imath].
c) Khi điểm [imath]\mathrm{A}[/imath] di chuyển trên cung lớn [imath]\mathrm{AB}[/imath], tìm vị trí của điểm [imath]\mathrm{A}[/imath] để diện tích tứ giác [imath]B I C D[/imath] đạt giá trị lớn nhất.
Attachments
Last edited: