 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
xem câu 4c đi bn mk vẽ thêm dường kính rồi gọi trung điểm chứng minh 5 điểm thuộc đường tròn v..vv mây mây nhưng vẫn ngộ nhậnCâu 5:
[tex]\left\{\begin{matrix} x(2x-2y+1)=y(1)\\y+2\sqrt{1-x-2x^{2}}=2(1+y^{2}) (2) \end{matrix}\right.[/tex]
ĐKXĐ: [tex]-1\leq x\leq \frac{1}{2}[/tex]
[tex]PT(1)\Leftrightarrow 2x(x-y)+(x-y)=0\Leftrightarrow (2x+1)(x-y)=0[/tex]
+) Th1: [tex]2x+1=0\Leftrightarrow x=\frac{-1}{2}[/tex](t/m)
Thay vào (2) được [tex]y+2=2(1+y^{2})\Leftrightarrow 2y^{2}-y=0\Leftrightarrow y(2y-1)=0\Leftrightarrow y=0[/tex] hoặc [tex]y=\frac{1}{2}[/tex]
+) Th2: [tex]x-y=0\Leftrightarrow x=y[/tex]
Thay vào (2) ta được:
$x+2\sqrt{1-x-2x^{2}}=2(1+x^{2})$
$\Leftrightarrow 2\sqrt{1-x-2x^{2}}=2+2x^{2}-x$ (ĐK: [tex]2+2x^{2}-x\geq 0[/tex])
$\Leftrightarrow 4(1-x-2x^{2})=(2+2x^{2}-x)^{2}$
$\Leftrightarrow 4x^{4}-4x^{3}+17x^{2}=0$
$\Leftrightarrow 4x^{2}(x^{2}-x+\frac{17}{4})=0$
$\Leftrightarrow x^{2}=0$ ( vì $x^{2}-x+\frac{17}{4}>0$)
$\Leftrightarrow x=0(t/m)$
[tex]\Rightarrow y=0[/tex]
Vậy...
bài này k tìm đk của y hả bạnCâu 5:
[tex]\left\{\begin{matrix} x(2x-2y+1)=y(1)\\y+2\sqrt{1-x-2x^{2}}=2(1+y^{2}) (2) \end{matrix}\right.[/tex]
ĐKXĐ: [tex]-1\leq x\leq \frac{1}{2}[/tex]
[tex]PT(1)\Leftrightarrow 2x(x-y)+(x-y)=0\Leftrightarrow (2x+1)(x-y)=0[/tex]
+) Th1: [tex]2x+1=0\Leftrightarrow x=\frac{-1}{2}[/tex](t/m)
Thay vào (2) được [tex]y+2=2(1+y^{2})\Leftrightarrow 2y^{2}-y=0\Leftrightarrow y(2y-1)=0\Leftrightarrow y=0[/tex] hoặc [tex]y=\frac{1}{2}[/tex]
+) Th2: [tex]x-y=0\Leftrightarrow x=y[/tex]
Thay vào (2) ta được:
$x+2\sqrt{1-x-2x^{2}}=2(1+x^{2})$
$\Leftrightarrow 2\sqrt{1-x-2x^{2}}=2+2x^{2}-x$ (ĐK: [tex]2+2x^{2}-x\geq 0[/tex])
$\Leftrightarrow 4(1-x-2x^{2})=(2+2x^{2}-x)^{2}$
$\Leftrightarrow 4x^{4}-4x^{3}+17x^{2}=0$
$\Leftrightarrow 4x^{2}(x^{2}-x+\frac{17}{4})=0$
$\Leftrightarrow x^{2}=0$ ( vì $x^{2}-x+\frac{17}{4}>0$)
$\Leftrightarrow x=0(t/m)$
[tex]\Rightarrow y=0[/tex]
Vậy...
bn lm dc hết ko vậybài này k tìm đk của y hả bạn
#Ann Lee: Theo mình là không cần.
vế này lớn hơn 0 rồi mà(ĐK: 2+2x2−x≥02+2x2−x≥02+2x^{2}-x\geq 0)
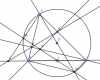
chắc được 0.5 bài này quáCâu 4c:
View attachment 58176
Hướng làm: ( chỉ là hướng thôi nhé, nên mình sẽ công nhận luôn những điều dễ c/m, có thời gian mình sẽ làm đầy đủ )
Gọi giao điểm của MH và (O) là D. Gọi I là trung điểm của BC
=> I cố định do BC không đổi
Vì KM.KA=KE.KF (câu b) nên tứ giác AMFE nội tiếp
Mà tứ giác AFHE nội tiếp
=> 5 điểm A,M,F,H,E cùng thuộc 1 đường tròn
=> Tứ giác AMHE nội tiếp
=> [tex]\widehat{AMH}+\widehat{AEH}=180^{\circ}\Rightarrow \widehat{AMH}=90^{\circ}[/tex]
=> AD là đường kính của (O)
Có BH//CD ( cùng vuông góc với AC); CH//BD ( cùng vuông góc với AA)
=> Tứ giác BHCD là hình bình hành
=> HD và BC cắt nhau tại trung điểm của mỗi đường
=> HD đi qua trung điểm I cố định của BC
Hay MH luôn đi qua điểm I cố định. (đpcm)
bài nào vậy bnTh1 có TM k
[tex]m=\frac{17}{9}[/tex]câu 2b bạn đc kết quả ntn??????
3
bài này mik lm dài ko bt có bị trừ điểm ko nữaCâu 4c:
View attachment 58176
Hướng làm: ( chỉ là hướng thôi nhé, nên mình sẽ công nhận luôn những điều dễ c/m, có thời gian mình sẽ làm đầy đủ )
Gọi giao điểm của MH và (O) là D. Gọi I là trung điểm của BC
=> I cố định do BC không đổi
Vì KM.KA=KE.KF (câu b) nên tứ giác AMFE nội tiếp
Mà tứ giác AFHE nội tiếp
=> 5 điểm A,M,F,H,E cùng thuộc 1 đường tròn
=> Tứ giác AMHE nội tiếp
=> [tex]\widehat{AMH}+\widehat{AEH}=180^{\circ}\Rightarrow \widehat{AMH}=90^{\circ}[/tex]
=> AD là đường kính của (O)
Có BH//CD ( cùng vuông góc với AC); CH//BD ( cùng vuông góc với AA)
=> Tứ giác BHCD là hình bình hành
=> HD và BC cắt nhau tại trung điểm của mỗi đường
=> HD đi qua trung điểm I cố định của BC
Hay MH luôn đi qua điểm I cố định. (đpcm)
4c Trang làm đc akbài này mik lm dài ko bt có bị trừ điểm ko nữa
ukm nhưng dài , lm sang tờ thứ 3 lun4c Trang làm đc ak
Hợp lý thì chắc có điểm mà nghe nói chỉ có Kim Chi, Hoàng Đạo làm đc bài này thôi phải k?ukm nhưng dài , lm sang tờ thứ 3 lun
Hợp lý thì chắc có điểm mà nghe nói chỉ có Kim Chi, Hoàng Đạo làm đc bài này thôi phải k?
mấy bn huyện nào vậyuk nhưng đạo câu 5 sai
mà ai nsHợp lý thì chắc có điểm mà nghe nói chỉ có Kim Chi, Hoàng Đạo làm đc bài này thôi phải k?

