Đề thi tuyển sinh vào 10 - Toán chung - Long An - Năm học: 2019 - 2020
Mời các bạn tham khảo!
View attachment 115895
Câu I.
1. $K=\sqrt{9}+\sqrt{45}-3\sqrt{5} \\
= 3+3\sqrt{5}-3\sqrt{5}=3$
3. ĐK: $x^2+4x+4 \neq 0 \\
\Leftrightarrow x \neq -2
$
Bình phương 2 vế ta được:
$x^2+4x+4 =9 \\
\Leftrightarrow x^2+4x-5=0 \\
\Leftrightarrow x_1=1;x_2=-5
$
Câu II.
2. Phương trình hoành độ giao điểm:
$2x^2=2x+4 \\
\Leftrightarrow 2x^2-2x-4=0 \\
\Leftrightarrow x_1=-1;x_2=2$
Thay $x_1;x_2$ vào $(d)$ ta được $y_1=2;y_2=8$
Vậy có 2 giao điểm là $(-1;2)$ và $(2;8)$
3. $(d')$ song song với $(d) \Leftrightarrow \left\{\begin{matrix}
a=a' & \\
b \neq b' &
\end{matrix}\right. \\
\\
\Leftrightarrow \left\{\begin{matrix}
a=2 & \\
b \neq 4&
\end{matrix}\right.$
$(d')$ đi qua $N(2;3) \Leftrightarrow x=2;y=3 \\
\Leftrightarrow 3=2.2+b \\
\Leftrightarrow b=-1$
Câu III:
1. Giải $\Delta$ tìm nghiệm. $x_1=5;x_2=2$
2. Dùng phương pháp cộng đại số. $x=2;y=-1$
3a)
$\Delta'=b'^2-ac \\
=(-3)^2-1.m \\
=9-m$
Phương trình có 2 nghiệm phân biệt $\Leftrightarrow \Delta' \geq 0 \\
\Leftrightarrow 9-m \geq 0 \\
\Leftrightarrow m \leq 9$
Câu IV:
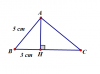
1. $AH=\sqrt{AB^2-BH^2} \\
\\
=\sqrt{5^2-3^2}=4(cm)$
Ta có :$AB^2=BH.BC \\
\\
\Leftrightarrow 5^2=3.BC \\
\\
\Leftrightarrow BC=\frac{25}{3}(cm)$
$AC=\sqrt{AH^2+HC^2} \\
=\sqrt{4^2+(\frac{16}{3})^2}=\frac{20}{3}(cm)$
$sin\widehat{CAH}=\frac{HC}{AC}=\frac{16}{3} : \frac{20}{3}=\frac{4}{5}$
2. Hình vẽ tham khảo
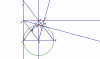
a) $\widehat{PAO}+\widehat{PMO}=180^o$
Suy ra tứ giác APMP nội tiếp.
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.




