C
cobetuoiteen
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
KỲ THI TUYỂN SINH VÀO LỚP 10 MÔN TOÁN TỈNH KHÁNH HÒA 2008-2009
THỜI GIAN :120P'
Bài 1: (3đ) (học sinh ko dùng máy tính càm tay để giải bài 1)
a)Tính giá trị biểu thức :
A=[tex]5\sqrt{12} -4 \sqrt{75} +2 \sqrt{48} -3\sqrt{3}[/tex]
b)Giải hệ pt:
[tex]\left\{ \begin{array}{l} 2x+y= 3\\ 3x - y =2 \end{array} \right.[/tex]
c)Giải pt: x^4-7x^2-18= 0
Bài 2: (2đ)
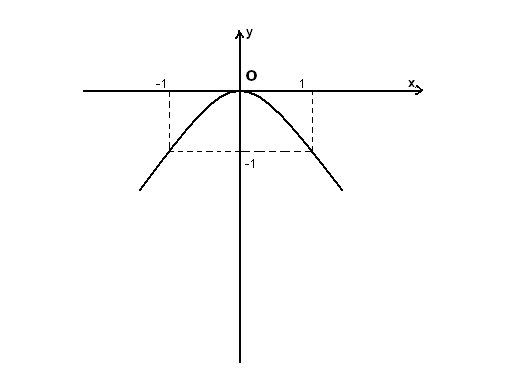
Cho hàm số y=-x^2 có đồ thị(P) và y=2x-3 có đồ thị (d)
a)vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy
b)Bằng phương pháp đại số, xác định tọa độ gaio điểm của (P) và (d).
Bài 3: (1đ)
Lập phương trình bậc 2 ẩn x có 2 nghiệm x1, x2 thỏa mãn điều kiện:
x1+x2 = và [tex]\frac{1}{x1-1}[/tex]+[tex]\frac{1}{x2-1}[/tex]
Bài 4: (4đ)
Cho tam giác ABC vuông tại A. Kẻ đường cao AH và đường phân giác BE (H thuộc BC, E thuộc AC).kẻ AD vuông góc với BE(D thuộc BE)
a)Chứng minh tứ giác ADHB nội tiếp được.Xác định tâm O của đường tròn (O) ngoại tiếp tứ giác ADHB.
b)Chứng minh tứ giác ODCB là hình thang.
c)Gọi I là giao điểm của OD và AH.Chứng minh:
[tex]\frac{1}{AH^2}[/tex]=[tex]\frac{1}{AB^2}[/tex]+[tex]\frac{1}{AC^2}[/tex]
d)Cho biết góc ABC = 60 độ, độ dài AB = a.Tính theo a diện tích phần giới hạn bởi AC, BC và cung nhỏ AH của (O).
-------------HẾT-----------
> < >
< > < >
< > < >
< > < >
< > <
<
CHÚC CÁC BẠN LÀM BÀI TỐT
TỰ TIN+ BÌNH TĨNH= WIN
%%-%%-%%-%%-%%-%%-%%-%%-%%-%%-%%-
THỜI GIAN :120P'
Bài 1: (3đ) (học sinh ko dùng máy tính càm tay để giải bài 1)
a)Tính giá trị biểu thức :
A=[tex]5\sqrt{12} -4 \sqrt{75} +2 \sqrt{48} -3\sqrt{3}[/tex]
b)Giải hệ pt:
[tex]\left\{ \begin{array}{l} 2x+y= 3\\ 3x - y =2 \end{array} \right.[/tex]
c)Giải pt: x^4-7x^2-18= 0
Bài 2: (2đ)
Cho hàm số y=-x^2 có đồ thị(P) và y=2x-3 có đồ thị (d)
a)vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy
b)Bằng phương pháp đại số, xác định tọa độ gaio điểm của (P) và (d).
Bài 3: (1đ)
Lập phương trình bậc 2 ẩn x có 2 nghiệm x1, x2 thỏa mãn điều kiện:
x1+x2 = và [tex]\frac{1}{x1-1}[/tex]+[tex]\frac{1}{x2-1}[/tex]
Bài 4: (4đ)
Cho tam giác ABC vuông tại A. Kẻ đường cao AH và đường phân giác BE (H thuộc BC, E thuộc AC).kẻ AD vuông góc với BE(D thuộc BE)
a)Chứng minh tứ giác ADHB nội tiếp được.Xác định tâm O của đường tròn (O) ngoại tiếp tứ giác ADHB.
b)Chứng minh tứ giác ODCB là hình thang.
c)Gọi I là giao điểm của OD và AH.Chứng minh:
[tex]\frac{1}{AH^2}[/tex]=[tex]\frac{1}{AB^2}[/tex]+[tex]\frac{1}{AC^2}[/tex]
d)Cho biết góc ABC = 60 độ, độ dài AB = a.Tính theo a diện tích phần giới hạn bởi AC, BC và cung nhỏ AH của (O).
-------------HẾT-----------
>
CHÚC CÁC BẠN LÀM BÀI TỐT
TỰ TIN+ BÌNH TĨNH= WIN
%%-%%-%%-%%-%%-%%-%%-%%-%%-%%-%%-