1.
a.
ĐK: $x\ne \pm 2$.
$ \dfrac{2x-1}{x^2-4}+\dfrac{x+3}{2-x}+5=0\\\Leftrightarrow \dfrac{2x-1}{x^2-4}+\dfrac{-x^2-5x-6}{x^2-4}+\dfrac{5x^2-20}{x^2-4}=0\\\Leftrightarrow \dfrac{2x-1-x^2-5x-6+5x^2-20}{x^2-4}=0\\\Leftrightarrow \dfrac{4x^2-3x-27}{x^2-4}=0\\\Leftrightarrow 4x^2-3x-27=0\\\Delta=441\\\Rightarrow x_1=3;x_2=-\dfrac{9}{4} $.
Vậy phương trình có 2 nghiệm là $ x=3 $ hoặc $x=-\dfrac{9}{4}$.
b.
Gọi $x$ (giờ) $(x>0)$ là thời gian người thứ nhất xây xong bức tường.
Theo đề ta có:
Thời gian người thứ hai xây xong bức tường là $x+6$ (giờ).
Mỗi giờ người thứ nhất xây được $ \dfrac{1}{x} $ bức tường.
Mỗi giờ người thứ hai xây được $ \dfrac{1}{x+6} $ bức tường.
Theo đề ta có phương trình:
$ \dfrac{4}{x}+\dfrac{12}{x+6}=1 \\\Leftrightarrow \dfrac{4(x+6)+12x}{x(x+6)}=1\\\Leftrightarrow 16x+24=x^2+6x\\\Leftrightarrow x^2-10x-24=0 \\\Leftrightarrow (x+2)(x-12)=0 \\\Rightarrow
\left[\begin{matrix}
x+2=0\\
x-12=0
\end{matrix}\right. \\\Leftrightarrow
\left[\begin{matrix}
x=-2(loại)\\
x=12(nhận)
\end{matrix}\right.
$.
$ \Rightarrow $ Thời gian người thứ hai xây xong bức tường là $ 12+6=18 $(giờ).
Vậy thời gian người thứ nhất, người thứ hai xây xong bức tường lần lượt là $ 12 $ giờ và $ 18 $ giờ.
2.
a.
Ta có phương trình hoành độ giao điểm:
$ x^2=2(m-1)x+m+1\\\Leftrightarrow x^2-2(m-1)x-(m+1)=0\\\Delta_x'=[-(m-1)]^2-1[-(m+1)]=m^2-2m+1+m+1=m^2-m+2=\left (m-\dfrac12 \right )^2+\dfrac{7}{4}\ge \dfrac{7}{4} > 0 \forall m\in \mathbb{R} $.
Vậy $ (d) $ luôn cắt $(P)$ tại $2$ điểm phân biệt với mọi $m$.
b.
Áp dụng hệ thức Viét:
$ x_1+x_2=\dfrac{-[2(m-1)]}{1}=2m-2 \\x_1x_2=\dfrac{-(m+1)}{1}=-m-1(*)$.
Và $ x_1+3x_2-8=0\Leftrightarrow x_1+3x_2=8$.
Giải hệ phương trình:
$
\left\{\begin{matrix}
x_1+x_2=2m-2\\
x_1+3x_2=8
\end{matrix}\right.\\\Leftrightarrow \left\{\begin{matrix}
x_1+x_2=2m-2\\
2x_2=-2m+10
\end{matrix}\right.\\\Leftrightarrow \left\{\begin{matrix}
x_1=3m-7\\
x_2=-m+5
\end{matrix}\right. $.
Thay vào $(*)$ ta có:
$ (3m-7)(-m+5)=-m-1\\\Leftrightarrow -3m^2+22m-35=-m-1\\\Leftrightarrow -3m^2+23m-34=0 $.
$ \Delta_m=(23)^2-4(-3)(-34)=121 $.
$ \Rightarrow m_1=\dfrac{-23+\sqrt{121}}{-6}=2; m_2 =\dfrac{-23-\sqrt{121}}{-6}=\dfrac{17}{3} $.
3.
a.
$ A=\dfrac{1}{1+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+...+\dfrac{1}{\sqrt{2017}+\sqrt{2018}}\\=\dfrac{\sqrt{2}-1}{(1+\sqrt{2})(\sqrt{2}-1)}+\dfrac{\sqrt{3}-\sqrt{2}}{(\sqrt{2}+\sqrt{3})(\sqrt{3}-\sqrt{2})}+...+\dfrac{\sqrt{2018}-\sqrt{2017}}{(\sqrt{2017}+\sqrt{2018})(\sqrt{2018}-\sqrt{2017})}\\=\sqrt{2}-1+\sqrt{3}-\sqrt{2}+...+\sqrt{2018}-\sqrt{2017}\\=\sqrt{2018}-1 $.
b.
$ 1+\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{2017}}\\=2.\left ( \dfrac{1}{2}+\dfrac{1}{2\sqrt{2}}+\dfrac{1}{2\sqrt{3}}+...+\dfrac{1}{2\sqrt{2017}} \right )\\Đặt \ D=\dfrac{1}{2}+\dfrac{1}{2\sqrt{2}}+\dfrac{1}{2\sqrt{3}}+...+\dfrac{1}{2\sqrt{2017}}\\Có:\\\dfrac{1}{2}=\dfrac{1}{1+1}>\dfrac{1}{1+\sqrt{2}}\\\dfrac{1}{2\sqrt{2}}=\dfrac{1}{\sqrt{2}+\sqrt{2}}>\dfrac{1}{\sqrt{2}+\sqrt{3}}\\...\\\dfrac{1}{2\sqrt{2017}}=\dfrac{1}{\sqrt{2017}+\sqrt{2017}}>\dfrac{1}{\sqrt{2017}+\sqrt{2018}}\\\Rightarrow D>\dfrac{1}{1+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+...+\dfrac{1}{\sqrt{2017}+\sqrt{2018}}\\\Rightarrow D>\sqrt{2}-1+\sqrt{3}-\sqrt{2}+...+\sqrt{2018}=\sqrt{2018}-1\\\Rightarrow 2D=1+\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{2017}}>2(\sqrt{2018}-1) $.
4.
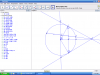
View attachment 57975
PS: Hình nãy bị lỗi + hơi nhỏ.
a.
$ H $ là trung điểm $ AB $.
$ \Rightarrow OH \perp AB $
$ \Rightarrow \widehat{OHM}=90^o$.
$ \widehat{OCM}=\widehat{ODM}=90^o(gt)$.
TH1: $ D $ và $ H $ đối nhau.
Ta có: $ \widehat{ODM}+\widehat{OHM}=90^o+90^o=180^o$.
$ \Rightarrow ODMH $ nội tiếp đường tròn.
$\Rightarrow O,D,M,H $ cùng thuộc một đường tròn.
TH2: $ D $ và $ H $ kề nhau.
Ta có: $ \hat{D} $ và $ \hat{H} $ đều nhìn $ OM $ dưới một góc vuông nên $ ODMH $ nội tiếp đường tròn.
$ \Rightarrow O,D,M,H $ cùng thuộc một đường tròn.
b.
Gọi $ K $ là giao điểm của $ OM $ và $ CD $.
$ OI = OD = OC $ (cùng là bán kính của $ (O;R) $).
$ OI = OD (cmt)\Rightarrow \widehat{OID}=\widehat{ODI} $.
$ OD = OC (cmt); MD = MC $ (tính chất của hai tiếp tuyến cắt nhau).
$ \Rightarrow OM $ là đường trung trực của $ CD$.
$ \Rightarrow OM \perp CD $.
Xét $ \triangle DKI, \hat{K} = 90^o $ ta có:
$ \widehat{KID}+\widehat{KDI}=90^o$.
$ \widehat{ODI}+\widehat{IDM}=\widehat{ODM}=90^o(gt) $.
$ \Rightarrow \widehat{ODI}+\widehat{IDM}=\widehat{KID}+\widehat{KDI} (=90^o) $.
mà $\widehat{OID}=\widehat{ODI} $.
$ \Rightarrow \widehat{IDM}=\widehat{KDI} $.
$ \Rightarrow DI $ là phân giác của $\widehat{CDM} $.
Lại có: $ MI $ là phân giác của $ \widehat{CMD} $ (tính chất của hai tiếp tuyến cắt nhau).
$ \Rightarrow I $ là tâm đường tròn nội tiếp của $ \triangle CDM $.
c.
Thua =_=.
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
