M
minhtuyb
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Đề thi HMEO <Đề chính thức>
--Bảng B--
--Bảng B--
Câu 1:
a)(3 đ) Chứng minh rẳng $A=(2^n-1)(2^n+1)$ chia hết cho $3$ với mọi số tự nhiên $n$
b)(4 đ) Chứng minh rằng $2^{2p}+2^{2q}$ không thể là số chính phương với mọi $p,q$ là các số nguyên không âm
Câu 2: Giải các phương trình, hệ phương trình sau:
$a)\ (3,5 d) \ x^4+9=5x(3-x^2)$
$b\ (3,5 d) \left\{\begin{matrix}x+y+z=6\\ xy+yz+zx=-1\\ x^2+y^2+z^2=14\end{matrix}\right.$
Câu 3: (7 đ) Cho hai hàm số:
$$A(x)=x^3+ax^2+bx+c\\ B(x)=x^2+x+2012$$
Biết rằng phương trình $A(x)=0$ có 3 nghiệm phân biệt và phương trình $A\left [ B(x) \right ]=0$ vô nghiệm.
Chứng minh rằng: $\large{A(2012)>\frac{1}{64}}$
Câu 4:
a) (3 đ) Cho hai điểm $A(2;3)$ và $B(7;7)$ trên mặt phẳng toạ độ $Oxy$. Tìm điểm $M$ nằm trên trục $Ox$ để $MA+MB$ đạt GTNN. Tìm GTNN đó.
b) (4 đ) Trên mặt phẳng toạ độ $Oxy$ cho 3 hàm số sau:
$$(1): y=-x+1\\ (2): y=x-1\\ (3):y=-ax+a^3-a^2-\frac{1}{3}$$
(Với $a$ là tham số)
Tìm $a$ để đồ thị của 3 hàm số trên đồng quy.
Câu 5:
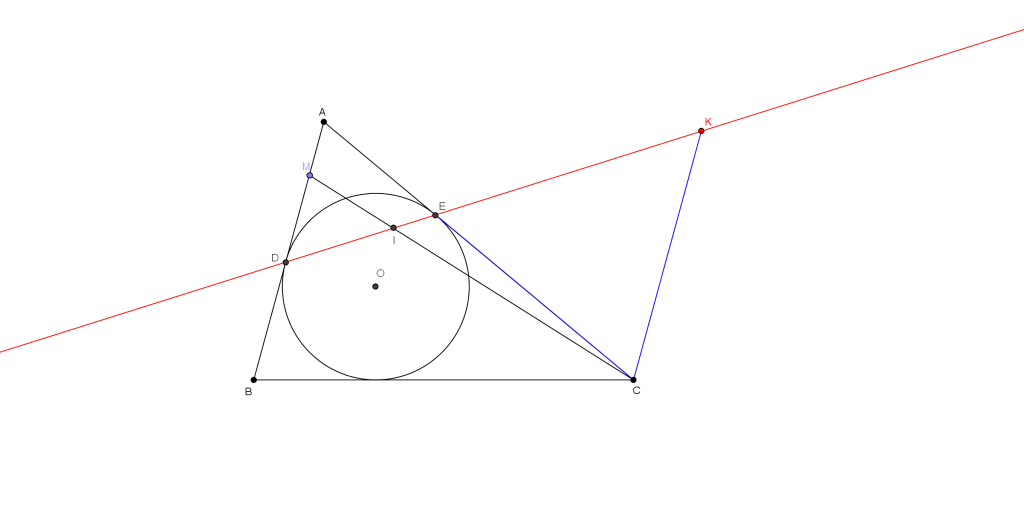
a) (4 đ) Cho $\Delta ABC$ nhọn ngoại tiếp đường tròn $(O)$ tiếp xúc với $AB,AC$ lần lượt tại $D,E$. Lấy $M$ bất kì trên đoạn $AD$ khác $A,D$. $CM$ cắt $DE$ tại $I$.
Chứng minh rằng: $\large{\frac{IM}{IC}=\frac{DM}{CE}}$
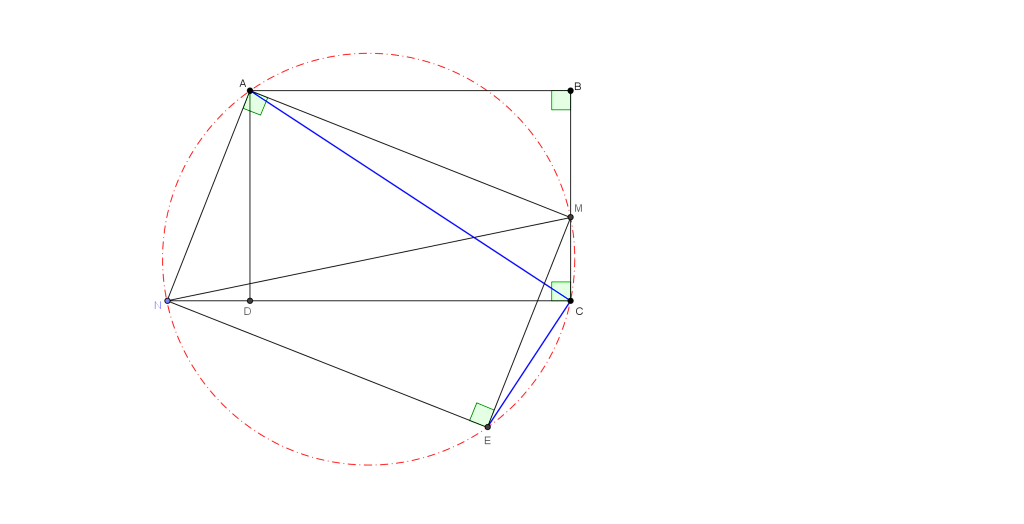
b) (3 đ) Cho hình chữ nhật $ABCD$. Một góc vuông $xAy$ quay xung quanh $A$. Các tia $Ax,Ay$ lần lượt cắt đoạn thẳng $BC$, đường thẳng $CD$ tại $M,N$. Gọi $E$ là đỉnh thứ tư của hình chứ nhật $MANE$
Chứng minh rằng: $AC\perp CE$
Câu 6: (7 đ) Chứng minh rằng trong đa giác lồi $2n$ cạnh $n\in \mathbb{N}, n\ge 2$, luôn tồn tại ít nhất $n$ đường chéo không song song với bất kì cạnh nào của đa giác đó
--------------------------HẾT--------------------------
Câu 6 trong đề này khá phổ biến. Xin lỗi vì sai sót này của mình. Vòng sau BTC sẽ tự ra đề và đáp án nên sẽ không còn trường hợp này xảy ra nữa 
Cảm ơn mọi người đã ủng hộ. Đáp án chính thức sẽ được đăng vào ngày 19-20/07/2012. Trong thời gian này mọi người cứ giải đề tự nhiên nhé ;
Cảm ơn mọi người đã ủng hộ. Đáp án chính thức sẽ được đăng vào ngày 19-20/07/2012. Trong thời gian này mọi người cứ giải đề tự nhiên nhé ;