Câu 4: Hình vẽ:
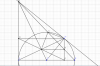
a) $QMPA$ là hình chữ nhật $\Rightarrow$ I là trung điểm AM.
$EA$ và $EM$ là tiếp tuyến $(O)$ $\Rightarrow$ $EA= EM$
$\Rightarrow$$E$ thuộc đường trung trực của AM.
Ta có: $OA=OB=R$$\Rightarrow$$O$ thuộc đường trung trực của $AB$.
Nên $E,I,O$ thẳng hàng.
b) Ta có: $QM.ME=QM.EA=2.S_{EMA}$
Do $AO=OB$ nên $MP.AO=MP.OB=MP.OM$ hay $2.S_{MAO}=2.S_{MOB}$.
$QM.ME+MP.OB=2.S_{EMA}+2.S_{MAO}=2S_{EAOM}=EO.AM=EO.QP$(đpcm).
c) Ta có: $\Delta EMC \sim \Delta EBM$
$\Rightarrow$ $EC.EB=EM^2$.
và $EI.EO=EM^2$
$\Rightarrow$$EI.EO=EC.EB$
$\Rightarrow$$ICBO$ nội tiếp.
$\Rightarrow$$\widehat{ICB}=\widehat{IOA}$ hay $\widehat{ICK}=\widehat{IOA}$(1)
Dễ c/m cho: $\widehat{IOA}=\widehat{IMK}$(2)
Từ (1) và (2)$\Rightarrow$$\widehat{ICK}=\widehat{IMK}$
$\Rightarrow$$ICMK$ nội tiếp$\Rightarrow$$\widehat{CKI}=\widehat{CMI}$ hay$\widehat{CKI}=\widehat{CMA}$.(3)
Lại có: $\widehat{CMA}=\widehat{CBA}$ (2 góc nt cùng chắn cung CA)(4)
Từ (3) và (4)$\Rightarrow$$\widehat{CKI}=\widehat{CBA}$.
Hai góc này ở vị trí đồng vị$\Rightarrow$$IK//AB$.
Xét $\Delta MAP$: $IK//AP; I$ là trung điểm AM$\Rightarrow$IK là đường tb
$\Rightarrow$ K là trung điểm MP.
d) Do $\Delta APM \sim \Delta AMB$ nên $S_{AQMP}=2.S_{AMP}$ là lớn nhất khi $2.S_{AMB}$ lớn nhất.
Ta có: $2.S_{AMB}=AM.MB\leq\frac{AM^2+MB^2}{2}=\frac{R^2}{2}$
Dấu "=" xảy ra khi $AM=MB$$\Rightarrow$M là điểm chính giữa cung AB
$\Rightarrow$[tex]P\equiv O[/tex].
$\Rightarrow$ $x=R$
Khi đó: $S_{AQMP}=AP.PM=AO.OM=R^2$.
Không biết có sai không nữa...
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
