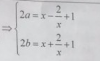Có đáp án không vậy ? Câu 1.2, 2.a và bài 5 thì làm kiểu gì vậy ?
2.a
Từ đề bài suy ra [TEX]x^2-2^n=80[/TEX]. Ta thấy ngay [TEX]n[/TEX] là số tự nhiên. Nhận thấy [TEX]x[/TEX] và [TEX]-x[/TEX] đều là nghiệm nên ta chỉ xét [TEX]x[/TEX] không âm.
Ta chứng minh được [TEX]n[/TEX] chẵn (Hãy phản chứng [TEX]n[/TEX] lẻ, xét đồng dư mod 5 suy ra vô lí).
Đặt [TEX]n=2a[/TEX] với [TEX]a[/TEX] là số tự nhiên.
Thế thì biến đổi về [TEX](x-2^a)(x+2^a)=80[/TEX]. Thế là xong rồi!
Chú ý một chút: Mình có nói xét [TEX]x[/TEX] không âm thực chất là để hạn chế tối đa số trường hợp phải xét khi có được phương trình ước số [TEX](x-2^a)(x+2^a)=80[/TEX].
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.