Câu 1
1)
Đặt $x^2=y(y\geq 0)$
=>$y^2+9y=0$
<=>$y(y+9)=0$
<=>[tex]\left\{\begin{matrix} y=0(thỏamãn)\\ y=-9(không thỏa mãn) \end{matrix}\right.[/tex]
=> x = 0
2)
a)[tex]\frac{\sqrt{x}}{\sqrt{x}+3}+\frac{2\sqrt{x}}{\sqrt{x}-3}-\frac{3x+9}{x-9}=\frac{(x-3\sqrt{x})+(2x+6\sqrt{x})-(3x+9)}{(\sqrt{x}+3)(\sqrt{x}-3)}=\frac{x-3\sqrt{x}+2x+6\sqrt{x}-3x-9}{(\sqrt{x}+3)(\sqrt{x}-3)}=\frac{3\sqrt{x}-9}{(\sqrt{x}+3)(\sqrt{x}-3)}=\frac{3}{\sqrt{x}+3}[/tex]
b)[tex]\frac{3}{\sqrt{x}+3}=\frac{1}{3}\Leftrightarrow \sqrt{x}+3=9\Leftrightarrow \sqrt{x}=6\Leftrightarrow x=36[/tex]
Câu 2
a)
b)
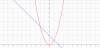
Hoành độ giao điểm của (d) và (P) là hai nghiệm của phương trình
[tex]x^2=-x+2\Leftrightarrow x^2+x-2=0[/tex]
[tex]\Leftrightarrow \Delta =1+4.2=9[/tex]
[tex]\left\{\begin{matrix} x_1=\frac{-1-\sqrt{9}}{2}=-2\\ x_2=\frac{-1+\sqrt{9}}{2}=1 \end{matrix}\right.[/tex]
[tex]\Rightarrow \left\{\begin{matrix} y_1=x_1^2=4\\ y_2=x_2^2=1 \end{matrix}\right.[/tex]
Vậy tọa độ của hai giao điểm là A(-2;4) ; B(1;1)
Câu 3)
1)
[tex]\left\{\begin{matrix} 3x-2y=5\\ x+3y=7 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 3x-2y=5\\ 3x+9y=21 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 3x-2y=5\\ -11y=-16 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=\frac{29}{11}\\ y=\frac{16}{11} \end{matrix}\right.[/tex]
2)
a)[tex]x^2-(m+5)x+3m+6=0[/tex]
[tex]\Delta =(m+5)^2-4(3m+6)=m^2+10m+25-12m-24=m^2-2m+1=(m-1)^2≥0[/tex]
Vậy phương trình luôn có nghiệm với [tex]\forall m[/tex]
b)
Do $x_1$ và $x_2$ là 2 cạnh của một tam giác vuông có cạnh huyền
Áp dụng định lý Pi - ta - go
[tex]x_1^2+x_2^2=5^2=25[/tex]
[tex]\Leftrightarrow (x_1+x_2)^2-2x_1x_2=25(1)[/tex]
Theo hệ thức Vi-ét
[tex]\left\{\begin{matrix} x_1+x_2=m+5\\ x_1x_2=3m+6 \end{matrix}\right.[/tex]
Do $x_1>0$, $x_2>0$
=>[tex]\left\{\begin{matrix} x_1+x_2=m+5>0\\ x_1x_2=3m+6 >0\end{matrix}\right.\Leftrightarrow m>-2[/tex]
thay $x_1+x_2=m+5$ , $x_1x_2=3m+6$ vào (1)
[tex]\Leftrightarrow (m+5)^2-2(3m+6)=25\Leftrightarrow m^2+10m+25-6m-12=25\Leftrightarrow m^2+4m-12=0[/tex]
[tex]\Delta '=2^2+12=16[/tex]
=>[tex]\left\{\begin{matrix} m_1=-2+\sqrt{16}=2\\ m_2=-2-\sqrt{16}=-6(loại) \end{matrix}\right.[/tex]
Câu 4
Đổi: 3h 20 phút =10/3h
Gọi thời gian của mỗi công nhân nếu làm riêng lần lượt là x và y (x,y>0)
=> năng xuất mỗi người trong một giờ là
[tex]\left\{\begin{matrix} \frac{1}{x}=X\\ \frac{1}{y}=Y \end{matrix}\right.[/tex] (công việc)
do trong cả hai trường hợp hai người đều làm xong công việc
=> [tex]6(X+Y)=\frac{10}{3}X+10Y\Leftrightarrow \frac{8}{3}X-4Y=0[/tex](1)
mặt khác, do cả hai người làm chung xong cong việc trong 6h => mỗi giờ hai người làm được
[tex]X+Y=\frac{1}{6}[/tex] (2)
Giải hệ phương trình (1),(2)
=>[tex]\left\{\begin{matrix} X=\frac{1}{10}\\ Y=\frac{1}{15} \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=10(h)\\ y=15(h) \end{matrix}\right.[/tex]
Câu 4)
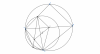
a)Chứng minh đường trung bình EO của tam giác ABC, đường trung bình FO của tam giác ABD
=>[tex]\widehat{AEO}=\widehat{ACB}=90^o[/tex]
=>[tex]\widehat{AFO}=\widehat{ADB}=90^o[/tex]
=>[tex]\widehat{AFO}+\widehat{AEO}=180^o[/tex]
=> AEOF nội tiếp
Xét tính chất đường tròn ngoại tiếp tam giác vuông => tâm đường tròn là trung điểm của OA
b)Theo định lý Pi-ta-go
=> [tex]AC^2+CB^2=AB^2=AD^2+DB^2[/tex]
xin lỗi, câu c mình không giải được
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.



