đề kiểm tra chất ượng đầu năm ( đà lạt )

[ruacon2705]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

sửa dùm đề kt nhé ^^
câu 1: chứng minh
[TEX]<a href="http://www.codecogs.com/eqnedit.php?latex=\frac{1@plus; cos4x @plus; sin4x}{1 - cos4x @plus; sin4x}= cot2x" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\frac{1+ cos4x + sin4x}{1 - cos4x + sin4x}= cot2x" title="\frac{1+ cos4x + sin4x}{1 - cos4x + sin4x}= cot2x" /></a>[/TEX]

Câu 2: giải bất pt:

Câu 3: giải pt
a)

b)

c)

câu 4:giá trị lớn nhất, nhỏ nhất của hàm số sau

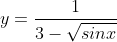
câu 5:
trong mặt phẳng toạ độ Oxy, cho hai điểm A(3;5), B(-1;-1) và

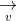có tọa độ (-2;3)
1) Viết phương trình ( C ) đường kính AB
2) Viết phương trình ( C' ) là ảnh của ( C ) qua phép tịnh tiến theo

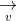
QUÁ DỄ, BÀI NÀY KHÔNG ĐƯỢC 7 ĐIỂM THÌ HƠI UỔNG, MẤY BẠN LÀM THỬ NHÉ ^^!

 

[thien0526]

câu 1:
[TEX]VT=\frac{1+cos4x+sin4x}{1-cos4x+sin4x}[/TEX]
[TEX]=\frac{2cos^2 2x +2sin2xcos2x}{2sin^2 2x+2sin2xcos2x}[/TEX]
[TEX]= \frac{2cos2x(cos2x+sin2x)}{2sin2x(sin2x+cos2x)}[/TEX]
[TEX]=\frac{cos2x}{sin2x}=cot2x=VP[/TEX]

 

[thien0526]

câu 3:
[TEX]a) sin(x-\frac{\pi}{3})=\frac{-\sqrt{3}}{2}[/TEX]
[TEX]\Leftrightarrow sin(x-\frac{\pi}{3})=-sin(\frac{\pi}{3})=sin(\frac{-\pi}{3}[/TEX]
[TEX]\Leftrightarrow \left[\begin{x-\frac{\pi}{3}=\frac{-\pi}{3}+k2\pi}\\{x-\frac{\pi}{3}=\frac{4\pi}{3}+k2\pi} [/TEX]
[TEX]\Leftrightarrow \left[\begin{x=k2\pi}\\{x = \frac{5\pi}{3}+k2\pi} [/TEX]

[TEX]b) cos(2x+15^o)=\frac{-1}{2}[/TEX]
[TEX]\Leftrightarrow cos(2x+15^o)=-cos(30^o)=cos(150^o)[/TEX]
[TEX]\Leftrightarrow \left[\begin{2x+15^o=150^o+k360^o}\\{2x+15^o=-150^o+k360^o} [/TEX]
[TEX]\Leftrightarrow \left[\begin{x=(\frac{135}{2})^o+k180^o}\\{x=(\frac{-165}{2})^o+k180^o} [/TEX]

[TEX]c)\frac{tanx}{1+cos3x}=0 (1)[/TEX]
ĐK:[TEX]\left{\begin{cosx\not=\0}\\{1+cos3x \not= \ 0}[/TEX]
[TEX]\Leftrightarrow \left{\begin{x \not=\ \frac{\pi}{2}+k\pi}\\{x \not=\ \frac{\pi}{3}+k\frac{2\pi}{3}}[/TEX]
với điều kiên trên ta có
[TEX](1)\Leftrightarrow tanx=0[/TEX]
[TEX]\Leftrightarrow sinx=0[/TEX]
[TEX]\Leftrightarrow x=t\pi[/TEX]
Đối chiếu vs điều kiên ta được [tex] x=t2\pi[/tex]

 

[thien0526]

câu 4:
ĐK: [TEX]sinx\geq 0[/TEX]
Vs đk trên ta có
[TEX]\forall x\in\ \mathbb{R}, 0\leq\sqrt{sinx}\leq1[/TEX]
[TEX]\Leftrightarrow 3\geq 3-\sqrt{sinx}\geq 2[/TEX]
Ta có
*[TEX]y=\frac{1}{3} \Leftrightarrow sinx=0 \Leftrightarrow x=k\pi[/TEX]
Vậy [TEX]y_{min}=\frac{1}{3} \Leftrightarrow x=k\pi[/TEX]
*[TEX]y=\frac{1}{2} \Leftrightarrow sinx=1 \Leftrightarrow x=\frac{\pi}{2}+k2\pi[/TEX]
Vậy [TEX]y_{max}=\frac{1}{2} \Leftrightarrow x=\frac{\pi}{2}+k2\pi[/TEX]


câu5:
a) PT đường tròn (C) có dạng [TEX](x-x_o)^2+(y-y_o)^2=R^2[/TEX]
(C) có tâm [TEX]I(x_o;y_o)[/TEX] và bán kính [TEX]R[/TEX]
(C) có đường kính là AB[TEX]\Rightarrow[/TEX]tâm I của đường tròn là trung điểm của AB
[TEX]\Rightarrow[/TEX]I(1;2)
(C) có bán kính R với: [TEX]R^2=IA^2=(3-1)^2+(5-2)^2=13[/TEX]
Vậy PT đường tròn (C) là [TEX](x-1)^2+(y-2)^2=13[/TEX]
b) Gọi [TEX](C')=T_v (C)[/TEX]
(C') có pt dạng [TEX](x-x_1)^2+(y-y_1)^2=R_1^2[/TEX], (C') có tâm [TEX]I_1(x_1;y_1)[/TEX] và bán kính [TEX]R_1[/TEX]
Thì ta có [TEX]\left{\begin{I_1 = T_v (I)\\{R_1=R} [/TEX]
[TEX]\Leftrightarrow \left{\begin{I_1 (-1;-1)}\\{R_1^2 =13}[/TEX]
Vậy (C') có PT là [TEX](x+1)^2+(y+1)^2=13[/TEX]