P
philong92
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Môn thi : Toán – Lớp 12
Thời gian : 150 phút
-------------------------------------------------
Câu I (2 điểm)Cho hàm số:
 (H)
(H)
1. Giải bất phương trình :
\sqrt{{{x}^{2}}-4x+3}\ge 0)
2. Giải phương trình :
\left( 3\sin x-\sqrt{3} \right)={{\sin}^{2}}x-\frac{1}{2}\sin 2x)
3. Giải hệ phương trình :
=x-3\sqrt[3]{2x-1} \\ \end{align}\right.)
Câu III (2 điểm)

2. Cho x,y là các số thực thỏa mãn
;y\le 0) .
.
Tìm giá trị lớn nhất , giá trị nhỏ nhất của
+3{{x}^{2}}-3x+2)
Câu IV (2 điểm)
1. Trong mặt phẳng Oxy, cho hình bình hành ABCD có diện tích bằng 4. Biết A(1;0), B(0;2) và giao điểm I của hai đường chéo nằm trên đường thẳng y = x. Tìm tọa độ đỉnh C và D.
2. Cho hình chóp S.ABC có các mặt bên hợp với đáy góc 600 , góc

 . Tính thể tích khối chóp S.ABC
. Tính thể tích khối chóp S.ABC
Phần tự chọn ( Thí sinh chỉ được làm một trong hai câu V.1 hoặc V.2)Câu V.1.(1 điểm) Cho a, b, c là các số thực dương thay đổi thỏa mãn:
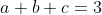 .
.
Chứng minh rằng :
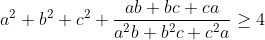
Câu V.2.(1 điểm) Chứng minh rằng với mọi số thực x,y ta có :
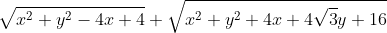
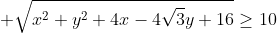
------ Hết -------
Thời gian : 150 phút
-------------------------------------------------
Câu I (2 điểm)Cho hàm số:
- <LI class="MsoNormal
 ">Khảo sát sự biến thiên và vẽ đồ thị (H) của hàm số.
">Khảo sát sự biến thiên và vẽ đồ thị (H) của hàm số. - Tiếp tuyến của (H) tại M có tung độ bằng
cắt Ox,Oy lần lượt tại A,B. Tính độ dài đoạn thẳng AB
1. Giải bất phương trình :
2. Giải phương trình :
3. Giải hệ phương trình :
Câu III (2 điểm)
- Tính giới hạn sau :
2. Cho x,y là các số thực thỏa mãn
Tìm giá trị lớn nhất , giá trị nhỏ nhất của
Câu IV (2 điểm)
1. Trong mặt phẳng Oxy, cho hình bình hành ABCD có diện tích bằng 4. Biết A(1;0), B(0;2) và giao điểm I của hai đường chéo nằm trên đường thẳng y = x. Tìm tọa độ đỉnh C và D.
2. Cho hình chóp S.ABC có các mặt bên hợp với đáy góc 600 , góc
Phần tự chọn ( Thí sinh chỉ được làm một trong hai câu V.1 hoặc V.2)Câu V.1.(1 điểm) Cho a, b, c là các số thực dương thay đổi thỏa mãn:
Chứng minh rằng :
Câu V.2.(1 điểm) Chứng minh rằng với mọi số thực x,y ta có :
------ Hết -------

