- 19 Tháng sáu 2017
- 1,170
- 1,126
- 201
- 22
- Bình Định
- Đại học Khoa Học Tự Nhiên - ĐHQG TPHCM
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
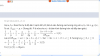
Bài 1. (6,0 điểm)
1.Giải phương trình [tex]\sqrt{3x+1}+\sqrt{5x+4}=3x^2-x+3[/tex]
2.Giải hệ phương trình [tex]\left\{\begin{matrix} x^2+x^3y-xy^2+xy-y=1 & \\ x^4+y^2-xy(2x-1)=1 & \end{matrix}\right.[/tex]
Bài 2. (3,0 điểm) Chứng mình rằng nếu phương trình [tex]x^4+bx^3+cx^2+bx+1=0[/tex] có nghiệm thì :
[tex]b^2+(c-2)^2>3[/tex]
Bài 3. (3,0 điểm) Cho hai số thuwcsk [tex]a,b[/tex] [tex]\epsilon[/tex] [tex]\left [ -1;1 \right ][/tex] . Chứng mình rằng
[tex]\left | a\sqrt{1-b^2}+b\sqrt{1-a^2}-\sqrt{3}\left [ ab-\sqrt{(1-a^2(1-b^2)} \right ] \right |\leqslant 2[/tex]
Bài 4. (3,0 điểm) Cho tam giác ABC có độ dài các đường cao là những số nguyên và bán kính đường tròn nội tiếp bằng 1 . Chứng minh rằng tam giác ABC là tam giác đều.
Bài 5. (5,0 điểm)
1.Trong mặt phẳng [tex]Oxy[/tex] , cho tam giác ABC cân tại A[tex](-1;3)[/tex]. Gọi D là điểm trên cạnh AB sao cho AB=3AD và H là hình chiếu vuông góc của B trên CD . Điểm M[tex]\left ( \frac{1}{2};\frac{-3}{2} \right )[/tex] là trung điểm đoạn HC . Xác định tọa độ đỉnh C , biết đỉnh B nằm trên đường thằng có phương trình [tex]x+y+7=0[/tex]
2. Cho tam giác ABC có [tex]BC=a;CA=b;BA=c[/tex] [tex]\left ( b\neq c \right )[/tex] và diện tích là S . Kí hiệu [tex]m_{a}[/tex] ; [tex]m_{b}[/tex] ; [tex]m_{c}[/tex] lần lượt là độ dài của các đường trung tuyến kẻ từ các đỉnh A,B,C. Biết rằng [tex]2 m_{a}^2\geqslant m_{b}^2+m_{c}^2.[/tex]
a. Chứng minh rằng [tex]a^2\leqslant 4S.cotA[/tex]
b. Gọi O và G lần lượt là tâm đường tròn ngoại tiếp và trọng tâm tam giác ABC; M là trung điểm của BC. Chứng minh rằng góc [tex]\widehat{MGO}[/tex] không nhọn
1.Giải phương trình [tex]\sqrt{3x+1}+\sqrt{5x+4}=3x^2-x+3[/tex]
2.Giải hệ phương trình [tex]\left\{\begin{matrix} x^2+x^3y-xy^2+xy-y=1 & \\ x^4+y^2-xy(2x-1)=1 & \end{matrix}\right.[/tex]
Bài 2. (3,0 điểm) Chứng mình rằng nếu phương trình [tex]x^4+bx^3+cx^2+bx+1=0[/tex] có nghiệm thì :
[tex]b^2+(c-2)^2>3[/tex]
Bài 3. (3,0 điểm) Cho hai số thuwcsk [tex]a,b[/tex] [tex]\epsilon[/tex] [tex]\left [ -1;1 \right ][/tex] . Chứng mình rằng
[tex]\left | a\sqrt{1-b^2}+b\sqrt{1-a^2}-\sqrt{3}\left [ ab-\sqrt{(1-a^2(1-b^2)} \right ] \right |\leqslant 2[/tex]
Bài 4. (3,0 điểm) Cho tam giác ABC có độ dài các đường cao là những số nguyên và bán kính đường tròn nội tiếp bằng 1 . Chứng minh rằng tam giác ABC là tam giác đều.
Bài 5. (5,0 điểm)
1.Trong mặt phẳng [tex]Oxy[/tex] , cho tam giác ABC cân tại A[tex](-1;3)[/tex]. Gọi D là điểm trên cạnh AB sao cho AB=3AD và H là hình chiếu vuông góc của B trên CD . Điểm M[tex]\left ( \frac{1}{2};\frac{-3}{2} \right )[/tex] là trung điểm đoạn HC . Xác định tọa độ đỉnh C , biết đỉnh B nằm trên đường thằng có phương trình [tex]x+y+7=0[/tex]
2. Cho tam giác ABC có [tex]BC=a;CA=b;BA=c[/tex] [tex]\left ( b\neq c \right )[/tex] và diện tích là S . Kí hiệu [tex]m_{a}[/tex] ; [tex]m_{b}[/tex] ; [tex]m_{c}[/tex] lần lượt là độ dài của các đường trung tuyến kẻ từ các đỉnh A,B,C. Biết rằng [tex]2 m_{a}^2\geqslant m_{b}^2+m_{c}^2.[/tex]
a. Chứng minh rằng [tex]a^2\leqslant 4S.cotA[/tex]
b. Gọi O và G lần lượt là tâm đường tròn ngoại tiếp và trọng tâm tam giác ABC; M là trung điểm của BC. Chứng minh rằng góc [tex]\widehat{MGO}[/tex] không nhọn
