[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
1. Tìm các giá trị nguyên dương của m để hệ phương trình [tex]\left\{\begin{matrix} \\ x - my =3 \\ mx - y = -3 \end{matrix}\right.[/tex] có nghiệm nguyên
2. Cho 2 đường tròn (O;4cm) và (O';3cm) có OO' = 5cm, hai đường tròn cắt nhau tại A,B. Tính độ dài AB
3. Gọi S là tập hợp các giá trị của tham số m để phương trình [tex]x^{2} - (m-1) + m-3=0[/tex] có 2 nghiệm [tex]x_{1}[/tex], [tex]x_{2}[/tex] thỏa mãn [tex]x_{1}x_{2}^{2}+x_{2}x_{1}^{2}[/tex] = 3. Tìm các phần tử thuộc tập hợp S và tính tổng bình phương các phần tử của tập hợp S
4. Biết rằng tồn tại giá trị của tham số m để phương trình [tex]x^{2}-2(m+1)x+m^{2}+3=0[/tex] có 2 nghiệm [tex]x_{1}[/tex], [tex]x_{2}[/tex] sao cho biểu thức S = [tex]x_{1}x_{2}+x_{1}+x_{2}[/tex] có giá trị nhỏ nhất. Tìm giá trị nhỏ nhất của S
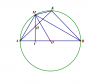
5. Cho đường tròn (O), đường kính AB = 2R. Gọi C là trung điểm của OA, dây MN vuông góc AB tại C. Trên cung nhỏ MB lấy điểm K, nối AK cắt MN tại H. Tính tích của AH và AK theo R
6. Cho các số dương x,y,z thỏa mãn: [tex]x\sqrt{1-y^{2}}+y\sqrt{1-z^{2}}+z\sqrt{1-x^{2}}=\frac{3}{2}[/tex]. Tính giá trị của biểu thức A = [tex]x^{2}+y^{2}+z^{2}[/tex]
giúp em với ạ
2. Cho 2 đường tròn (O;4cm) và (O';3cm) có OO' = 5cm, hai đường tròn cắt nhau tại A,B. Tính độ dài AB
3. Gọi S là tập hợp các giá trị của tham số m để phương trình [tex]x^{2} - (m-1) + m-3=0[/tex] có 2 nghiệm [tex]x_{1}[/tex], [tex]x_{2}[/tex] thỏa mãn [tex]x_{1}x_{2}^{2}+x_{2}x_{1}^{2}[/tex] = 3. Tìm các phần tử thuộc tập hợp S và tính tổng bình phương các phần tử của tập hợp S
4. Biết rằng tồn tại giá trị của tham số m để phương trình [tex]x^{2}-2(m+1)x+m^{2}+3=0[/tex] có 2 nghiệm [tex]x_{1}[/tex], [tex]x_{2}[/tex] sao cho biểu thức S = [tex]x_{1}x_{2}+x_{1}+x_{2}[/tex] có giá trị nhỏ nhất. Tìm giá trị nhỏ nhất của S
5. Cho đường tròn (O), đường kính AB = 2R. Gọi C là trung điểm của OA, dây MN vuông góc AB tại C. Trên cung nhỏ MB lấy điểm K, nối AK cắt MN tại H. Tính tích của AH và AK theo R
6. Cho các số dương x,y,z thỏa mãn: [tex]x\sqrt{1-y^{2}}+y\sqrt{1-z^{2}}+z\sqrt{1-x^{2}}=\frac{3}{2}[/tex]. Tính giá trị của biểu thức A = [tex]x^{2}+y^{2}+z^{2}[/tex]
giúp em với ạ