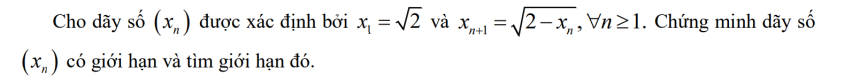Dễ thấy [imath]x_n \in (0,\sqrt{2}) \forall n \in \mathbb{N}^*[/imath]
Đặt [imath]f(x)=\sqrt{2-x}[/imath] thì [imath]f[/imath] là hàm nghịch biến.
[imath]\Rightarrow f(f(x))[/imath] đồng biến.
Từ đó ta có [imath]x_1=\sqrt{2}, x_2=\sqrt{2-\sqrt{2}},x_3=\sqrt{2-\sqrt{2-\sqrt{2}}} < \sqrt{2}[/imath] nên [imath]x_1>x_3[/imath]
[imath]\Rightarrow x_1>x_3>...>x_{2n+1}[/imath]
Mà [imath]x_{2n+1}>0[/imath] nên [imath](x_{2n+1})[/imath] bị chặn dưới. Từ đó dãy [imath](x_{2n+1})[/imath] có giới hạn.
Đặt [imath]\lim x_{2n+1}=l \in (0,\sqrt{2-\sqrt{2}})[/imath] thì [imath]f(f(l))=l \Rightarrow \sqrt{2-\sqrt{2-l}}=l \Rightarrow l^2=2-\sqrt{2-l}[/imath]
[imath]\Rightarrow l^2-l=2-l-\sqrt{2-l}[/imath]
Xét [imath]g(x)=x^2-x[/imath]. Ta có [imath]g(x)=g(y) \Leftrightarrow \left[\begin{array}{l} x=y \\ x+y=1 \end{array}\right.[/imath]
Từ đó [imath]g(l)=g(\sqrt{2-l}) \Rightarrow \left[\begin{array}{l} l=\sqrt{2-l} \\ l+\sqrt{2-l}=1 \end{array}\right.[/imath]
Dễ thấy [imath]0<l<1 \Rightarrow l+\sqrt{2-l} =2+l-2+\sqrt{2-l}=\dfrac{9}{4}-(\sqrt{2-l}-\dfrac{1}{2})^2>1[/imath] nên phương trình thứ [imath]2[/imath] vô nghiệm.
[imath]l=\sqrt{2-l} \Leftrightarrow l^2+l-2=0 \Rightarrow \left[\begin{array}{l} l=1(tm) \\ l=-2(\text{loại}) \end{array}\right. \Rightarrow \lim x_{2n+1}=1[/imath]
Mặt khác, [imath]x_1<x_3 \Rightarrow f(x_1)>f(x_3) \Rightarrow x_2>x_4 \Rightarrow x_2>x_4>...>x_{2n}[/imath] nên [imath](x_{2n})[/imath] là dãy tăng.
Và [imath]x_{2n}<\sqrt{2}[/imath] nên [imath](x_{2n})[/imath] có giới hạn hữu hạn. Tương tự trên ta cũng có [imath]\lim x_{2n}=1[/imath].
Từ đó [imath]\lim x_n=1[/imath].
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé ^^ Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại đây nhé
Bài giảng Trường hè học sinh - giáo viên trường THPT chuyên 2022
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
