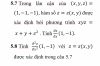Chuẩn rồi bạn. Dạng này gọi là "đạo hàm hàm ẩn".
Mình có một giải pháp hủy diệt được mọi bài mà không cần phải nhớ nhiều: lấy vi phân.
Không cần biết đề hỏi gì, bạn cứ lấy vi phân hai vế rồi tính gì tính tiếp:
$xyz = x + y + z^2$
$\implies yz \, dx + xz \, dy + xy \, dz = dx + dy + 2z \, dz$
Sau đó, thay $(x, y, z) = (1, -1, -1)$ để ra được $dx - dy - dz = dx + dy - 2 \, dz$, suy ra $dz = 0 \, dx + 2 \, dy$
Tới đây bạn sử dụng định nghĩa của đạo hàm từng phần hay vi phân toàn phần: $dz = \dfrac{\partial z}{\partial x} \, dx + \dfrac{\partial z}{\partial y} \, dy$, suy ra $\dfrac{\partial z}{\partial x} = 0$
Tương tự với đạo hàm từng phần cấp hai, nhưng trước khi thay số như trên, bạn có thể tính: $(xy - 2z) \, dz = (1 - yz) \, dx + (1 - xz) \, dy$, suy ra $\dfrac{\partial z}{\partial x} = \dfrac{1 - yz}{xy - 2z}$
Tới đây bạn lấy vi phân tương tự là được.
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.