- 27 Tháng mười 2018
- 3,742
- 3,706
- 561
- Hà Nội
- Trường Đại học Bách Khoa Hà Nội
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Dạng lượng giác của số phức được sử dụng nhằm khai căn số phức hoặc tính lũy thừa bậc cao của số phức một cách dễ dàng hơn.
Nó là 1 cách biểu diễn khác của số phức. Cụ thể ta đã biết số phức z=a+bi có điểm biểu diễn trên mp tọa độ Oxy là M(a;b)
Giờ ta gọi góc tạo bở OM và Ox là góc [tex]\theta[/tex]
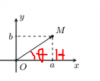
Như vậy, độ dài a đại diện cho phần thực, còn b đại diện cho phần ảo của số phức.
Ta có b=MH , a=OH , áp dụng lượng giác thì ta có:
[tex]a=OMcos\theta ; b=OMsin\theta[/tex]
Mà theo Pitago ta có: [tex]OM=\sqrt{a^2+b^2}[/tex]
Như vậy bây giờ số phức [tex]z=a+bi=\sqrt{a^2+b^2}(cos\theta+i. sin\theta)[/tex]
Đặt [tex]r=\sqrt{a^2+b^2}[/tex] , có thể thấy r là module của số phức z, lúc này z được biểu diễn dưới dạng lượng giác là: [tex]z=r(cos\theta+i.sin\theta)[/tex] với [TEX]\theta[/TEX] được gọi là 1 acgument của số phức z. Bởi vì tính chất tuần hoàn chu kì [tex]2\pi[/tex] của hàm cos và sin nên họ acgument của số phức z là :[tex]\theta+k2\pi (k\epsilon Z)[/tex]
[TEX]\theta[/TEX] được xác đinh bởi :
[tex]cos\theta=\frac{a}{\sqrt{a^2+b^2}}, sin\theta=\frac{b}{\sqrt{a^2+b^2}}[/tex]
Ví dụ: dạng lượng giác của số phức z=[tex]1+\sqrt{3}i[/tex] là?
Ta có : [tex]z=2(\frac{1}{2}+\frac{\sqrt{3}}{2}i)=2(cos\frac{\pi }{3}+sin\frac{\pi }{3})[/tex]
Vậy số phức z có module là 2 và Acgument là [TEX]\frac{\pi }{3}[/TEX]
Công thức Moa-Vrơ và ứng dụng.
Ta có công thức sau với dạng lượng giác của số phức:
[tex]z=r(cos\theta +i.sin\theta)=>z^n=r^n(cosn\theta+i.sinn\theta)[/tex]
Công thức này rất hữu dụng trong việc ta tính lũy thừa bậc cao hay khai căn của một số phức.
Trở lại ví dụ ban đầu, cho [tex]z=1+\sqrt{3}i[/tex] . Tính [tex]z^{10}[/tex]
Có thể thấy nếu như ta không đưa về lượng giác mà tính thông thường:
[tex](1+\sqrt{3}i)^{10}[/tex]
Thì việc klhai triển và tính toán mất rất nhiều thời gian, thậm chí không tính được. Tuy nhiên khi đưa về dạng lượng giác thì mọi chuyện lại rất dễ dàng:
[tex]z=2(cos\frac{\pi }{3}+i.sin\frac{\pi }{3})=>z^{10}=2^{10}(cos\frac{10\pi }{3}+i.sin\frac{10\pi }{3})[/tex]
Vậy cách làm chung với các bài toán tính bậc cao của số phức z, đó là đưa z về dạng lượng giác, sau đó áp dụng công thức Moa-Vrơ
Bài toán tính khai căn số phức.
Vẫn tương tự bài toán tính bậc cao của số phức, tuy nhiên có lưu ý nhỏ sau đây.
Vẫn sử dụng z đã cho ở trên, giờ ta tính [tex]\sqrt[4]{z}[/tex]
Ta có : [tex]\sqrt[4]{z}=z^{\frac{1}{4}}=2^{\frac{1}{4}}(cos(\frac{1}{4}\frac{\pi }{3}+\frac{k2\pi }{4})+i.sin(\frac{1}{4}\frac{\pi }{3}+\frac{k2\pi }{4}))=\sqrt[4]{2}(cos(\frac{\pi }{12}+\frac{k\pi }{2})+i.sin(\frac{\pi }{12}+\frac{k\pi }{2}))[/tex]
Như vậy lúc này thay 4 giá trị tương ứng là k=0,1,2,3 ta thu được 4 số phức tương ứng. Với k từ 4 trở đi thì chu kì lượng giác lại lặp lại
Vậy tại sao khi khai căn lại cần thêm họ acgument số phức, trong khi lũy thừa lên lại không cần. Đó là bởi vì khi lũy thừa lên ta có được họ acgument là [tex]n\theta +nk2\pi[/tex] . Lúc này [TEX]nk2\pi [/TEX] thì dù k bằng bao nhiêu thì vẫn là 1 số nguyên lần chu kì, không ảnh hưởng gì, nên bỏ đi
Còn khi khai căn thì họ acgument lúc này có: [tex]\frac{k2\pi }{n}[/tex] , với các k khác nhau từ 0 đến n-1, cho ta các số phức khác nhau.
Nói cách khác, thì lũy thừa của 1 số phức lên chỉ có 1 kết quả, còn khai căn bậc n số phức, cho ta n số phức kết quả.
Nó là 1 cách biểu diễn khác của số phức. Cụ thể ta đã biết số phức z=a+bi có điểm biểu diễn trên mp tọa độ Oxy là M(a;b)
Giờ ta gọi góc tạo bở OM và Ox là góc [tex]\theta[/tex]
Như vậy, độ dài a đại diện cho phần thực, còn b đại diện cho phần ảo của số phức.
Ta có b=MH , a=OH , áp dụng lượng giác thì ta có:
[tex]a=OMcos\theta ; b=OMsin\theta[/tex]
Mà theo Pitago ta có: [tex]OM=\sqrt{a^2+b^2}[/tex]
Như vậy bây giờ số phức [tex]z=a+bi=\sqrt{a^2+b^2}(cos\theta+i. sin\theta)[/tex]
Đặt [tex]r=\sqrt{a^2+b^2}[/tex] , có thể thấy r là module của số phức z, lúc này z được biểu diễn dưới dạng lượng giác là: [tex]z=r(cos\theta+i.sin\theta)[/tex] với [TEX]\theta[/TEX] được gọi là 1 acgument của số phức z. Bởi vì tính chất tuần hoàn chu kì [tex]2\pi[/tex] của hàm cos và sin nên họ acgument của số phức z là :[tex]\theta+k2\pi (k\epsilon Z)[/tex]
[TEX]\theta[/TEX] được xác đinh bởi :
[tex]cos\theta=\frac{a}{\sqrt{a^2+b^2}}, sin\theta=\frac{b}{\sqrt{a^2+b^2}}[/tex]
Ví dụ: dạng lượng giác của số phức z=[tex]1+\sqrt{3}i[/tex] là?
Ta có : [tex]z=2(\frac{1}{2}+\frac{\sqrt{3}}{2}i)=2(cos\frac{\pi }{3}+sin\frac{\pi }{3})[/tex]
Vậy số phức z có module là 2 và Acgument là [TEX]\frac{\pi }{3}[/TEX]
Công thức Moa-Vrơ và ứng dụng.
Ta có công thức sau với dạng lượng giác của số phức:
[tex]z=r(cos\theta +i.sin\theta)=>z^n=r^n(cosn\theta+i.sinn\theta)[/tex]
Công thức này rất hữu dụng trong việc ta tính lũy thừa bậc cao hay khai căn của một số phức.
Trở lại ví dụ ban đầu, cho [tex]z=1+\sqrt{3}i[/tex] . Tính [tex]z^{10}[/tex]
Có thể thấy nếu như ta không đưa về lượng giác mà tính thông thường:
[tex](1+\sqrt{3}i)^{10}[/tex]
Thì việc klhai triển và tính toán mất rất nhiều thời gian, thậm chí không tính được. Tuy nhiên khi đưa về dạng lượng giác thì mọi chuyện lại rất dễ dàng:
[tex]z=2(cos\frac{\pi }{3}+i.sin\frac{\pi }{3})=>z^{10}=2^{10}(cos\frac{10\pi }{3}+i.sin\frac{10\pi }{3})[/tex]
Vậy cách làm chung với các bài toán tính bậc cao của số phức z, đó là đưa z về dạng lượng giác, sau đó áp dụng công thức Moa-Vrơ
Bài toán tính khai căn số phức.
Vẫn tương tự bài toán tính bậc cao của số phức, tuy nhiên có lưu ý nhỏ sau đây.
Vẫn sử dụng z đã cho ở trên, giờ ta tính [tex]\sqrt[4]{z}[/tex]
Ta có : [tex]\sqrt[4]{z}=z^{\frac{1}{4}}=2^{\frac{1}{4}}(cos(\frac{1}{4}\frac{\pi }{3}+\frac{k2\pi }{4})+i.sin(\frac{1}{4}\frac{\pi }{3}+\frac{k2\pi }{4}))=\sqrt[4]{2}(cos(\frac{\pi }{12}+\frac{k\pi }{2})+i.sin(\frac{\pi }{12}+\frac{k\pi }{2}))[/tex]
Như vậy lúc này thay 4 giá trị tương ứng là k=0,1,2,3 ta thu được 4 số phức tương ứng. Với k từ 4 trở đi thì chu kì lượng giác lại lặp lại
Vậy tại sao khi khai căn lại cần thêm họ acgument số phức, trong khi lũy thừa lên lại không cần. Đó là bởi vì khi lũy thừa lên ta có được họ acgument là [tex]n\theta +nk2\pi[/tex] . Lúc này [TEX]nk2\pi [/TEX] thì dù k bằng bao nhiêu thì vẫn là 1 số nguyên lần chu kì, không ảnh hưởng gì, nên bỏ đi
Còn khi khai căn thì họ acgument lúc này có: [tex]\frac{k2\pi }{n}[/tex] , với các k khác nhau từ 0 đến n-1, cho ta các số phức khác nhau.
Nói cách khác, thì lũy thừa của 1 số phức lên chỉ có 1 kết quả, còn khai căn bậc n số phức, cho ta n số phức kết quả.
