- 27 Tháng mười 2018
- 3,742
- 3,706
- 561
- Hà Nội
- Trường Đại học Bách Khoa Hà Nội
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Dạng bài cho đồ thị hàm ẩn f ' (x) , xong yêu cầu tìm các thông tin liên quan của một hàm g(x) nào đó, 2 năm vừa rồi đều xuất hiện. Và chắc chắn năm nay cũng có.
Cụ thể cho dễ hình dung: trong đề thi thử sở Hà Nội chiều nay có 1 câu như thế này
Vậy cách làm dạng này như thế nào? Đối với ai mà chưa nắm dạng cơ bản của dạng nhìn đồ thị f ' (x) thì có thể tự tìm hiểu hoặc bài dạng cơ bản đó mình sẽ viết sau.
Đầu tiên, nói về giá trị lớn nhất, nhỏ nhất, thì cứ đạo hàm trước tiên:
[TEX]g'(x)= 2f'(x)-2(x-1)[/TEX]
Bây giờ mục đích đang muốn lập được BBT, vậy thì phải giải phương trình g'(x)=0
[tex]g'(x)=0<=>f'(x)=x-1[/tex]
Vậy đến đây, ta giải nó bằng cách vẽ đường thẳng y=x-1 vào trực tiếp tờ đề cho tiết kiệm thời gian
Vẽ đường thẳng không chỉ giúp giải nghiệm, mà còn giúp xét dấu nữa. Và đồ thị đường thẳng không khó vẽ, vậy nên mình mới nói đây là mức 1.
Với mức khó hơn thì cái đường cần vẽ không phải 1 đường thẳng, mà sẽ là 1 Parabol chẳng hạn
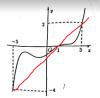
Cái đường đỏ đỏ là đường thẳng y=x-1. Có thể thấy rõ ràng là pt g'(x)=0 có 3 nghiệm phân biệt đó là x=-3, x=1, x=3
Vậy xét dấu thế nào để cho vào BBT?
Ta nhìn thấy trong đoạn từ -3 đến 1, đường đồ thị màu đỏ nằm thấp hơn so với hàm f ' (x) , có nghĩa:
g'(x) = f ' (x) - (x-1) >0 trong đoạn này
Tương tự g ' (x) <0 trong đoạn [1;3]
Vậy ta đưa vào BBT ( mình ko tiện vẽ ) sẽ thấy x= 1 sẽ là điểm cực đại, còn x=-3 và x=3 là 2 điểm thấp nhất trong đoạn [-3;3]
Do đó ta chỉ cần so sánh g(-3) với g(3) xem cái nào nhỏ hơn
Lúc này ta phải dùng đến tích phân: ta đã biết tích phân chính là tính diện tích hình phẳng giới hạn bởi 2 đường đồ thị hàm số.
Vậy : [tex]\int_{-3}^{3}g ' (x)dx=\int_{-3}^{3}(f'(x)-(x-1))dx=g(3)-g(-3)[/tex]
MÀ phần diện tích hình phẳng trong đoạn [-3;3] của 2 đồ thị, chia làm 2 khoảng như sau:
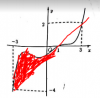
Từ [-3;1] nó là phần diện tích đỏ này, kí hiệu là S1(S1>0), phần diện tích đó dương do phần đồ thi f '(x) cao hơn (x-1)
Từ [1;3] nó là phần này
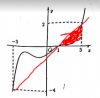
Và kết quả tích phân trả về , vì đồ thị hàm f ' (x) nằm thấp hơn. Gọi diện tích phần đó là S2(S2>0)
Vậy thì kết quả tích phân sẽ là : S1-S2
Mà bằng trực quan đồ thị, rõ ràng S1>S2 => S1-S2>0 , hay g(3)-g(-3)>0 <=> g(-3)<g(3)
Vậy kết luận giá trị nhỏ nhất là g(-3)
Ví dụ 2: ở bài này người ta vẫn cho f ' (x) nhưng mà có phần thay đổi nhỏ chút :
Lời giải:
Hỏi NB thì phải đạo hàm :
[tex]y'=-2f'(1-2x)+1-2x[/tex]
[tex]y'=0<=>f'(1-2x)=\frac{(1-2x)}{2}[/tex]
Rõ ràng rằng ta chỉ có f'(x) , vậy kiếm đâu ra f'(1-2x) mà giải. tuy nhiên để ý một chút, ta sẽ thấy dạng phương trình: [tex]f'(u)=\frac{u}{2} ; u=1-2x[/tex]
Như vậy lại áp dụng vẽ đường thẳng để giải nghiệm xét dấu được rồi. Ta vẽ đường bậc nhất y=x/2
Thấy pt có 3 nghiệm : x=0, x=2, x=4
Và tiến hành xét dấu : dấu của y' là dấu của:
[tex]\frac{u}{2}-f'(u)[/tex] , hàm NB khi [tex]\frac{u}{2}-f'(u) \leq 0[/tex]
Rõ ràng trong đoạn từ 2 đến 4 đường thẳng nằm thấp hơn nên [2;4] là khoảng NB của hàm y'
Giờ trả biến vì ta đã đặt u=1-2x : với u=2 ta được x=-1/2
Với u=4 ta được x=-3/2
Vậy ta chọn được khoảng NB thỏa mãn
Cụ thể cho dễ hình dung: trong đề thi thử sở Hà Nội chiều nay có 1 câu như thế này
Vậy cách làm dạng này như thế nào? Đối với ai mà chưa nắm dạng cơ bản của dạng nhìn đồ thị f ' (x) thì có thể tự tìm hiểu hoặc bài dạng cơ bản đó mình sẽ viết sau.
Đầu tiên, nói về giá trị lớn nhất, nhỏ nhất, thì cứ đạo hàm trước tiên:
[TEX]g'(x)= 2f'(x)-2(x-1)[/TEX]
Bây giờ mục đích đang muốn lập được BBT, vậy thì phải giải phương trình g'(x)=0
[tex]g'(x)=0<=>f'(x)=x-1[/tex]
Vậy đến đây, ta giải nó bằng cách vẽ đường thẳng y=x-1 vào trực tiếp tờ đề cho tiết kiệm thời gian
Vẽ đường thẳng không chỉ giúp giải nghiệm, mà còn giúp xét dấu nữa. Và đồ thị đường thẳng không khó vẽ, vậy nên mình mới nói đây là mức 1.
Với mức khó hơn thì cái đường cần vẽ không phải 1 đường thẳng, mà sẽ là 1 Parabol chẳng hạn
Cái đường đỏ đỏ là đường thẳng y=x-1. Có thể thấy rõ ràng là pt g'(x)=0 có 3 nghiệm phân biệt đó là x=-3, x=1, x=3
Vậy xét dấu thế nào để cho vào BBT?
Ta nhìn thấy trong đoạn từ -3 đến 1, đường đồ thị màu đỏ nằm thấp hơn so với hàm f ' (x) , có nghĩa:
g'(x) = f ' (x) - (x-1) >0 trong đoạn này
Tương tự g ' (x) <0 trong đoạn [1;3]
Vậy ta đưa vào BBT ( mình ko tiện vẽ ) sẽ thấy x= 1 sẽ là điểm cực đại, còn x=-3 và x=3 là 2 điểm thấp nhất trong đoạn [-3;3]
Do đó ta chỉ cần so sánh g(-3) với g(3) xem cái nào nhỏ hơn
Lúc này ta phải dùng đến tích phân: ta đã biết tích phân chính là tính diện tích hình phẳng giới hạn bởi 2 đường đồ thị hàm số.
Vậy : [tex]\int_{-3}^{3}g ' (x)dx=\int_{-3}^{3}(f'(x)-(x-1))dx=g(3)-g(-3)[/tex]
MÀ phần diện tích hình phẳng trong đoạn [-3;3] của 2 đồ thị, chia làm 2 khoảng như sau:
Từ [-3;1] nó là phần diện tích đỏ này, kí hiệu là S1(S1>0), phần diện tích đó dương do phần đồ thi f '(x) cao hơn (x-1)
Từ [1;3] nó là phần này
Và kết quả tích phân trả về , vì đồ thị hàm f ' (x) nằm thấp hơn. Gọi diện tích phần đó là S2(S2>0)
Vậy thì kết quả tích phân sẽ là : S1-S2
Mà bằng trực quan đồ thị, rõ ràng S1>S2 => S1-S2>0 , hay g(3)-g(-3)>0 <=> g(-3)<g(3)
Vậy kết luận giá trị nhỏ nhất là g(-3)
Ví dụ 2: ở bài này người ta vẫn cho f ' (x) nhưng mà có phần thay đổi nhỏ chút :
Lời giải:
Hỏi NB thì phải đạo hàm :
[tex]y'=-2f'(1-2x)+1-2x[/tex]
[tex]y'=0<=>f'(1-2x)=\frac{(1-2x)}{2}[/tex]
Rõ ràng rằng ta chỉ có f'(x) , vậy kiếm đâu ra f'(1-2x) mà giải. tuy nhiên để ý một chút, ta sẽ thấy dạng phương trình: [tex]f'(u)=\frac{u}{2} ; u=1-2x[/tex]
Như vậy lại áp dụng vẽ đường thẳng để giải nghiệm xét dấu được rồi. Ta vẽ đường bậc nhất y=x/2
Thấy pt có 3 nghiệm : x=0, x=2, x=4
Và tiến hành xét dấu : dấu của y' là dấu của:
[tex]\frac{u}{2}-f'(u)[/tex] , hàm NB khi [tex]\frac{u}{2}-f'(u) \leq 0[/tex]
Rõ ràng trong đoạn từ 2 đến 4 đường thẳng nằm thấp hơn nên [2;4] là khoảng NB của hàm y'
Giờ trả biến vì ta đã đặt u=1-2x : với u=2 ta được x=-1/2
Với u=4 ta được x=-3/2
Vậy ta chọn được khoảng NB thỏa mãn
