- 24 Tháng mười 2018
- 1,616
- 1,346
- 216
- 24
- TP Hồ Chí Minh
- Đại học Sư phạm Kỹ thuật TP Hồ Chí Minh
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
I. Hàm trùng phương
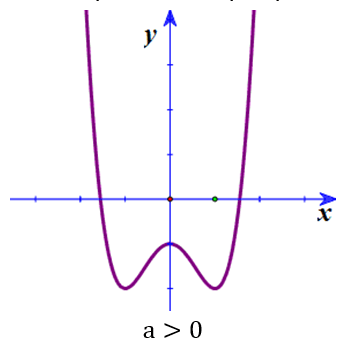
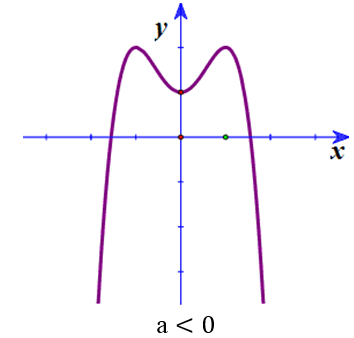
[tex]y=ax^4+bx^2+c[/tex] [tex](a\neq 0)[/tex]
đạo hàm: [tex]y'=4ax^3+2bx[/tex]
- hàm số có 3 điểm cực trị: [tex]a.b< 0[/tex]
- hàm số có 1 điểm cực trị: [tex]a.b\geq 0[/tex]
- hàm số có đúng 1 cực trị và cực trị là cực tiểu: [tex]\left\{\begin{matrix} a>0\\ b\geq 0 \end{matrix}\right.[/tex]
- hàm số có đúng 1 cực trị và cực trị là cực đại: [tex]\left\{\begin{matrix} a< 0\\ b\leq 0 \end{matrix}\right.[/tex]
- hàm số có 1 điểm cực đại và 2 điểm cực tiểu: [tex]\left\{\begin{matrix} a>0\\ b<0 \end{matrix}\right.[/tex]
- hàm số có 1 điểm cực tiểu và 2 điểm cực đại: [tex]\left\{\begin{matrix} a<0\\ b>0 \end{matrix}\right.[/tex]
- Giả sử đồ thị hàm số có 3 điểm cực trị là:
[tex]A(0;c);B(-\sqrt{\frac{-b}{2a}};-\frac{\Delta }{4a});C(\sqrt{\frac{-b}{2a}};-\frac{\Delta }{4a})[/tex]
khi đó A, B, C tạo thành một tam giác cân tại A với độ dài các cạnh lần lượt:
+ [tex]AB=AC=\sqrt{\frac{b^4}{16a^2}-\frac{b}{2a}}[/tex]
+ [tex]BC=2\sqrt{\frac{-b}{2a}}[/tex]
+ [tex]cos\widehat{A}=\frac{b^3+8a}{b^3-8a}[/tex]
II. Một số trường hợp thường gặp
đồ thị hàm số của hàm trùng phương có 3 điểm cực trị là A, B, C thỏa mãn một trong những điều kiện sau:
- [tex]\Delta ABC[/tex] vuông cân: [tex]\frac{b^3}{8a}+1=0[/tex]
- [tex]\Delta ABC[/tex] đều: [tex]\frac{b^3}{8a}+3=0[/tex]
- [tex]\widehat{BAC}=\alpha[/tex]: [tex]8a+b^3.tan^2\frac{\alpha }{2}=0[/tex]
- tạo thành tam giác có diện tích S: [tex]S^2=\frac{-b^5}{32a^3}[/tex]
- Bán kính đường tròn ngoại tiếp tam giác ABC là R: [tex]R=\frac{b^3-8a}{8|a|b}[/tex]
- tam giác ABC có [tex]BC=m_0[/tex]: [tex]am_0^2+2b=0[/tex]
- tam giác có [tex]AB=AC=n_0[/tex]: [tex]6a^2n_0^2-b^4+8ab=0[/tex]
- tam giác ABC có 2 đỉnh B, C nằm trên trục Ox: [tex]b^2=4ac[/tex]
- tam giác ABC là tam giác nhọn: [tex]b(8a+b^3)>0[/tex]
- tam giác ABC có trọng tâm là O: [tex]b^2=6ac[/tex]
- tam giác ABC có trực tâm là O: [tex]b^3+8a-4abc=0[/tex]
- tứ giác ABOC là hình thoi: [tex]b^2=2ac[/tex]
- tam giác ABC có O là tâm đường tròn ngoại tiếp: [tex]b^3-8a-8abc=0[/tex]
- tam giác ABC có O là tâm đường tròn nội tiếp: [tex]b^3-8a-4abc=0[/tex]
- trục hoành chia tam giác thành 2 phần có diện tích bằng nhau: [tex]b^2=4\sqrt{2}|ac|[/tex]
- đồ thị hàm số (C) cắt trục Ox tại 4 điểm lập thành cấp số cộng: [tex]\left\{\begin{matrix} b^2=\frac{100}{9}ac\\ \Delta >0\\ P> 0\\ S>0 \end{matrix}\right.[/tex]
- phương trình đường tròn ngoại tiếp: [tex]x^2+y^2-(\frac{2}{b}-\frac{\Delta}{4a}+c )y+(\frac{2}{b}-\frac{\Delta}{4a})c=0[/tex]
[tex]y=ax^4+bx^2+c[/tex] [tex](a\neq 0)[/tex]
đạo hàm: [tex]y'=4ax^3+2bx[/tex]
- hàm số có 3 điểm cực trị: [tex]a.b< 0[/tex]
- hàm số có 1 điểm cực trị: [tex]a.b\geq 0[/tex]
- hàm số có đúng 1 cực trị và cực trị là cực tiểu: [tex]\left\{\begin{matrix} a>0\\ b\geq 0 \end{matrix}\right.[/tex]
- hàm số có đúng 1 cực trị và cực trị là cực đại: [tex]\left\{\begin{matrix} a< 0\\ b\leq 0 \end{matrix}\right.[/tex]
- hàm số có 1 điểm cực đại và 2 điểm cực tiểu: [tex]\left\{\begin{matrix} a>0\\ b<0 \end{matrix}\right.[/tex]
- hàm số có 1 điểm cực tiểu và 2 điểm cực đại: [tex]\left\{\begin{matrix} a<0\\ b>0 \end{matrix}\right.[/tex]
- Giả sử đồ thị hàm số có 3 điểm cực trị là:
[tex]A(0;c);B(-\sqrt{\frac{-b}{2a}};-\frac{\Delta }{4a});C(\sqrt{\frac{-b}{2a}};-\frac{\Delta }{4a})[/tex]
khi đó A, B, C tạo thành một tam giác cân tại A với độ dài các cạnh lần lượt:
+ [tex]AB=AC=\sqrt{\frac{b^4}{16a^2}-\frac{b}{2a}}[/tex]
+ [tex]BC=2\sqrt{\frac{-b}{2a}}[/tex]
+ [tex]cos\widehat{A}=\frac{b^3+8a}{b^3-8a}[/tex]
II. Một số trường hợp thường gặp
đồ thị hàm số của hàm trùng phương có 3 điểm cực trị là A, B, C thỏa mãn một trong những điều kiện sau:
- [tex]\Delta ABC[/tex] vuông cân: [tex]\frac{b^3}{8a}+1=0[/tex]
- [tex]\Delta ABC[/tex] đều: [tex]\frac{b^3}{8a}+3=0[/tex]
- [tex]\widehat{BAC}=\alpha[/tex]: [tex]8a+b^3.tan^2\frac{\alpha }{2}=0[/tex]
- tạo thành tam giác có diện tích S: [tex]S^2=\frac{-b^5}{32a^3}[/tex]
- Bán kính đường tròn ngoại tiếp tam giác ABC là R: [tex]R=\frac{b^3-8a}{8|a|b}[/tex]
- tam giác ABC có [tex]BC=m_0[/tex]: [tex]am_0^2+2b=0[/tex]
- tam giác có [tex]AB=AC=n_0[/tex]: [tex]6a^2n_0^2-b^4+8ab=0[/tex]
- tam giác ABC có 2 đỉnh B, C nằm trên trục Ox: [tex]b^2=4ac[/tex]
- tam giác ABC là tam giác nhọn: [tex]b(8a+b^3)>0[/tex]
- tam giác ABC có trọng tâm là O: [tex]b^2=6ac[/tex]
- tam giác ABC có trực tâm là O: [tex]b^3+8a-4abc=0[/tex]
- tứ giác ABOC là hình thoi: [tex]b^2=2ac[/tex]
- tam giác ABC có O là tâm đường tròn ngoại tiếp: [tex]b^3-8a-8abc=0[/tex]
- tam giác ABC có O là tâm đường tròn nội tiếp: [tex]b^3-8a-4abc=0[/tex]
- trục hoành chia tam giác thành 2 phần có diện tích bằng nhau: [tex]b^2=4\sqrt{2}|ac|[/tex]
- đồ thị hàm số (C) cắt trục Ox tại 4 điểm lập thành cấp số cộng: [tex]\left\{\begin{matrix} b^2=\frac{100}{9}ac\\ \Delta >0\\ P> 0\\ S>0 \end{matrix}\right.[/tex]
- phương trình đường tròn ngoại tiếp: [tex]x^2+y^2-(\frac{2}{b}-\frac{\Delta}{4a}+c )y+(\frac{2}{b}-\frac{\Delta}{4a})c=0[/tex]
