Cho đoạn thẳng AD cố định. Gọi H là trung điểm AD. Kẻ đường thẳng d vuông góc AD tại D. Lấy điểm B, C nằm trên đường thẳng d sao cho tam giác ABC có H là trực tâm. Tìm vị trí của B, C sao cho BC ngắn nhất t/m đề bài.
Em xin chân thành cảm ơn!
Thực sự là tui không có chắc chắn về đáp án.
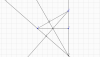
Gọi E, F lần lượt là chân đường cao hạ từ đỉnh C và B.
Ta có: $\Delta AEH \sim \Delta CDH$
$\Rightarrow \frac{AE}{CD}=\frac{HE}{HD}(1) \Rightarrow CD=\frac{AE.HD}{HE}$.
+) $\Delta AEH \sim \Delta ADB$
$\Rightarrow \frac{HE}{BD}=\frac{AE}{AD}(2)\Rightarrow BD=\frac{HE.AD}{AE}$.
$BC=BD+DC=\frac{AE.HD}{HE}+\frac{HE.AD}{AE}=\frac{AE.HD}{HE}+\frac{HE.2HD}{AE}$
$=HD.(\frac{AE}{HE}+2.\frac{HE}{AE})$.
Ta có: $\frac{AE}{HE}+2.\frac{HE}{AE} \geq 2.\sqrt{\frac{AE}{HE}.\frac{2HE}{AE}}=2\sqrt{2}$
$\Rightarrow BC \geq 2\sqrt{2}.HD=\sqrt{2}.AD$ (không đổi).
Dấu "=" xảy ra khi: $AE^2=2.HE^2 \Leftrightarrow AE=\sqrt{2}.HE(3)$
Từ (1) và (3)=> $CD=\sqrt{2}.HD=\frac{\sqrt{2}}{2}.AD$.
Từ (2) và (3)=> $BD=\frac{\sqrt{2}}{2}.AD$
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
