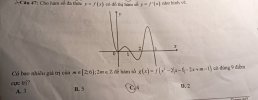Tìm m thoả mãn hàm số có 9 điểm cực trị
Le_Tuan_Anh 10
Ta có: [imath]g(x) = f(|x - 1|^2 - 2|x-1| + m-2)[/imath]
Đặt [imath]t = x-1 \to g(t) = f(|t|^2 - 2|t| + m -2)[/imath]
Xét [imath]h(t) = f(t^2 -2t + m -2)[/imath]
[imath]h'(t) = (2t-2)f'(t^2 -2t + m -2) = 0 \iff \left[\begin{array}{l} t = 1 \\ t^2 -2t + m -2 = 0 (nghiệm kép) \\t^2 -2t + m -2 = 1\\t^2 -2t + m -2 = 2\\t^2 -2t + m -2 = 3 \end{array}\right. \iff \left[\begin{array}{l} t = 1 \\ t^2 -2t = 2-m \\t^2 -2t = 3 - m \\t^2 -2t = 4-m \\t^2 -2t = 5-m \end{array}\right.[/imath]
Để [imath]g(t)[/imath] có 9 điểm cực trị thì [imath]h(t)[/imath] có đúng 4 điểm cực trị dương
TH1: Nghiệm kép là cực trị thì [imath]t = 1[/imath] là nghiệm của [imath]t^2 - 2t + m -2 = 0 \iff m = 3[/imath]
TH2: Nghiệm kép không là cực trị suy ra: [imath]3 - m > 0 \iff m <3[/imath]
Kết hợp điều kiện ta có: [imath]2 \le m < 3[/imath]
Vậy có [imath]3[/imath] giá trị [imath]m[/imath] thỏa mãn
Có gì không hiểu thì em hỏi lại nha
Ngoài ra, em tham khảo thêm kiến thức tại
Chinh phục kì thi THPTQG môn Toán 2022
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.