- 27 Tháng mười 2018
- 3,742
- 3,706
- 561
- Hà Nội
- Trường Đại học Bách Khoa Hà Nội
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Kiến thức cơ bản: Ta có thể dễ dàng thấy hàm y=f(|x|) là một hàm chẵn, do đó 2 nhánh của đồ thị đối xứng nhau qua trục Oy.
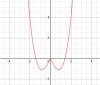
Ví dụ ở hình trên là 1 đồ thị của hàm chẵn.
Do tính đối xứng như chiếu qua 1 tấm gương, nên ta thấy nhánh đồ thị với x>0 có bao nhiêu cực trị, thì nhánh bên x<0 cũng có bấy nhiêu cực trị. Đồng thời tại x=0(với các hàm liên tục tại x=0) thì đồ thị luôn có một cực trị nữa. (Chỉ trừ trường hợp dạng hàm hằng như y=a, nhưng dạng hàm này không bao giờ gặp với bài toán này)
Từ đó ta thấy số cực trị có thể là: nếu với x>0 hàm có a cực trị thì trên toàn khoảng đang xét hàm có 2a+1 cực trị.
Bài tập:
1. Cho hàm số: [TEX]y=f(x)=x^3-3x^2-9x+2[/TEX]. Hỏi hàm số [TEX]f(|x|)[/TEX] có bao nhiêu cực trị?
Ta có: [TEX]f'(x)=3x^2-6x-9; f'(x)=0<=>x=-1[/TEX] hoặc [TEX]x=3[/TEX]
Xét với x>0 thì ta có: PT [TEX]f'(x)=0[/TEX] chỉ có 1 nghiệm x=3. Do đó hàm có 1 cực trị khi x>0
Vậy số cực trị của hàm f(|x|) trên R là: 1.2+1=3
2. Cho hàm số: [TEX]f(x)=x^3-3mx^2+3(m+1)x+1[/TEX]. Tìm m để hàm số f(|x|) có 5 cực trị
Giải: Ta có: [TEX]f'(x)=3x^2-6mx+3(m+1)[/TEX].
Xét x>0. Theo lý thuyết đã biết thì hàm f(|x|) có 5 cực trị chỉ khi hàm f(x) có 2 cực trị với x>0.
do đó PT [TEX]f'(x)=0<=>3x^2-6mx+3(m+1)=0[/TEX](1) phải có 2 nghiệm phân biệt dương.
[TEX](1)<=>x^2-2mx+(m+1)=0[/TEX]
Để PT có 2 nghiệm phân biệt dương thì:
[tex]\left\{\begin{matrix} \Delta '>0\\ S>0\\ P>0 \end{matrix}\right. <=>\left\{\begin{matrix} m^2-m-1>0\\ 2m>0\\ m+1>0 \end{matrix}\right. <=>m>\frac{1+\sqrt{5}}{2}[/tex]
3. Cho hàm số: [tex]y=f(x)=\frac{x^2-mx+6}{x-1}[/tex]. Tìm m để hàm số [TEX]y=f(|x|)[/TEX] có 5 cực trị.
Giải: Điều kiện: [TEX]x \neq 1[/TEX]
Ta có: [tex]y'=\frac{x^2-2x+m-6}{(x-1)^2}[/tex] (2)
Xét x>0. Để hàm có 5 cực trị thì pt (2) phải có 2 nghiệm phân biệt dương khác 1.
Xét điều kiện 2 nghiệm phân biệt dương:
[tex]\left\{\begin{matrix} \Delta '>0\\ S>0\\ P>0 \end{matrix}\right. <=>\left\{\begin{matrix} 7-m>0\\ 2>0\\ m-6>0 \end{matrix}\right. <=>6<m<7[/tex]
Điều kiện nghiệm khác 1: ta có: [TEX]1-2.1+m-6 \neq 0<=>m \neq 7[/TEX]
Vậy kết luận: 6<m<7 là điều kiện cần tìm.
Bên dưới là hình minh họa đồ thị với m=6,8
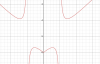
Ví dụ ở hình trên là 1 đồ thị của hàm chẵn.
Do tính đối xứng như chiếu qua 1 tấm gương, nên ta thấy nhánh đồ thị với x>0 có bao nhiêu cực trị, thì nhánh bên x<0 cũng có bấy nhiêu cực trị. Đồng thời tại x=0(với các hàm liên tục tại x=0) thì đồ thị luôn có một cực trị nữa. (Chỉ trừ trường hợp dạng hàm hằng như y=a, nhưng dạng hàm này không bao giờ gặp với bài toán này)
Từ đó ta thấy số cực trị có thể là: nếu với x>0 hàm có a cực trị thì trên toàn khoảng đang xét hàm có 2a+1 cực trị.
Bài tập:
1. Cho hàm số: [TEX]y=f(x)=x^3-3x^2-9x+2[/TEX]. Hỏi hàm số [TEX]f(|x|)[/TEX] có bao nhiêu cực trị?
Ta có: [TEX]f'(x)=3x^2-6x-9; f'(x)=0<=>x=-1[/TEX] hoặc [TEX]x=3[/TEX]
Xét với x>0 thì ta có: PT [TEX]f'(x)=0[/TEX] chỉ có 1 nghiệm x=3. Do đó hàm có 1 cực trị khi x>0
Vậy số cực trị của hàm f(|x|) trên R là: 1.2+1=3
2. Cho hàm số: [TEX]f(x)=x^3-3mx^2+3(m+1)x+1[/TEX]. Tìm m để hàm số f(|x|) có 5 cực trị
Giải: Ta có: [TEX]f'(x)=3x^2-6mx+3(m+1)[/TEX].
Xét x>0. Theo lý thuyết đã biết thì hàm f(|x|) có 5 cực trị chỉ khi hàm f(x) có 2 cực trị với x>0.
do đó PT [TEX]f'(x)=0<=>3x^2-6mx+3(m+1)=0[/TEX](1) phải có 2 nghiệm phân biệt dương.
[TEX](1)<=>x^2-2mx+(m+1)=0[/TEX]
Để PT có 2 nghiệm phân biệt dương thì:
[tex]\left\{\begin{matrix} \Delta '>0\\ S>0\\ P>0 \end{matrix}\right. <=>\left\{\begin{matrix} m^2-m-1>0\\ 2m>0\\ m+1>0 \end{matrix}\right. <=>m>\frac{1+\sqrt{5}}{2}[/tex]
3. Cho hàm số: [tex]y=f(x)=\frac{x^2-mx+6}{x-1}[/tex]. Tìm m để hàm số [TEX]y=f(|x|)[/TEX] có 5 cực trị.
Giải: Điều kiện: [TEX]x \neq 1[/TEX]
Ta có: [tex]y'=\frac{x^2-2x+m-6}{(x-1)^2}[/tex] (2)
Xét x>0. Để hàm có 5 cực trị thì pt (2) phải có 2 nghiệm phân biệt dương khác 1.
Xét điều kiện 2 nghiệm phân biệt dương:
[tex]\left\{\begin{matrix} \Delta '>0\\ S>0\\ P>0 \end{matrix}\right. <=>\left\{\begin{matrix} 7-m>0\\ 2>0\\ m-6>0 \end{matrix}\right. <=>6<m<7[/tex]
Điều kiện nghiệm khác 1: ta có: [TEX]1-2.1+m-6 \neq 0<=>m \neq 7[/TEX]
Vậy kết luận: 6<m<7 là điều kiện cần tìm.
Bên dưới là hình minh họa đồ thị với m=6,8
