- 27 Tháng mười 2018
- 3,742
- 3,706
- 561
- Hà Nội
- Trường Đại học Bách Khoa Hà Nội
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Với bài toán này, việc phá trị tuyệt đối để chia trường hợp và xét, là rất phức tạp. Do vậy, ta có thể áp dụng ghi nhớ sau:
Đặc điểm của hàm |f(x)| là: |f(x)|=f(x) khi [TEX]f(x) \geq 0[/TEX]
và |f(x)|= - f(x) khi [TEX]f(x)<0[/TEX]
Do đó phần đồ thị của f(x) nằm bên dưới Ox thì sẽ lấy đối xứng lên trên qua trục đối xứng là Ox.
Một phần nằm bên dưới Ox của đường thẳng y=x:
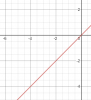
Khi lấy đối xứng lên qua trục Ox:
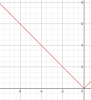
Do vậy, ta có 1 số kết luận sau:
+ Các cực trị của hàm f(x) cũng vẫn là cực trị của hàm |f(x)|
+ Các nghiệm bội lẻ của f(x) là cực trị của |f(x)| . ( thực ra nghiệm bội chẵn vẫn là cực trị thôi, nhưng nó cũng chính là cưc trị của f(x), nên khi đếm vào thì ta có thể đếm trùng )
=> Tổng số cực trị của hàm |f(x)| là số cực trị của f(x)+ số nghiệm bội lẻ của f(x).
Ví dụ : Số cực trị của hàm [tex]f(x)=|x^3-3x^2-9x|[/tex]
Xét hàm: [TEX]y=x^3-3x^2-9x[/TEX], [TEX]y'=3x^2-6x-9[/TEX]
[TEX]y'=0<=>x=-1; x=3[/TEX]
Vậy hàm y có 2 cực trị.
Sử dụng casio bấm nghiệm pt : [TEX]y=x^3-3x^2-9x[/TEX] có 3 nghiệm: [TEX]x=0;x=-1,85;x=4,85[/TEX]
=> Hàm f(x) có số cực trị là 3+2=5
Mô phỏng đồ thị của hàm:
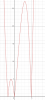
Vận dụng: Tìm giá trị của m để hàm số : [tex]f(x)=|x^4-x^3-5x^2+m|[/tex] có 7 điểm cực trị
Xét hàm [TEX]g(x)=x^4-x^3-5x^2+m[/TEX], ta có : [TEX]g'(x)=4x^3-3x^2-10x[/TEX]
[TEX]g'(x)=0<=>x=0,x=2,x=-5/4[/TEX]
Vậy hàm số f(x) có 3 điểm CT cũng là 3 điểm CT của g(x). Vậy để hàm f(x) có 7 điểm CT thì pt g(x)=0 có 4 nghiệm phân biệt.
Ta có: [TEX]g(x)=0<=>-x^4+x^3+5x^2=m[/TEX]
Xét hàm [TEX]v(x)=-x^4+x^3+5x^2[/TEX] , ta có BBT của hàm như sau:
Dựa vào BBT, ta thấy đường y=m cắt đồ thị v(x) tại 4 điểm phân biệt ( hay pt có 4 nghiệm phân biệt ) khi :
[TEX]0<m<\frac{875}{256}[/TEX]
Vận dụng 2: Tìm điều kiện của m để hàm số : [TEX]f(x)=(x^2+2)|x^2-m|[/TEX] có đúng 5 điểm cực trị
Đưa [TEX]x^2+2[/TEX] vào trong trị tuyệt đối ta có [TEX]f(x)=|(x^2+2)(x^2-m)|[/TEX]
Xét hàm g(x)=[TEX](x^2+2)(x^2-m)[/TEX] là hàm bậc 4, nên chỉ có tối đa 3 CT.
pt [TEX]g(x)=0[/TEX] chỉ có thể có nghiệm [TEX]x^2=m[/TEX]
Vậy nếu [TEX]m \leq 0[/TEX] thì pt g(x)=0 có tối đa 1 nghiệm => Có tối đa 4 CT, không thỏa mãn.
Vậy m>0 là điều kiện cần, khi đó g(x)=0 có 2 nghiệm : [tex]x=\sqrt{m},x=-\sqrt{m}[/tex]
Điều kiện đủ :
g(x) có 3 điểm CT khác với nghiệm của g(x)=0 :
[TEX]g(x)=x^4-(m-2)x^2-2m[/TEX], [TEX]g'(x)=4x^3-2(m-2)x[/TEX]
[TEX]g'(x)=0<=>x=0,[/TEX][tex]x=\sqrt{\frac{m-2}{2}},x=-\sqrt{\frac{m-2}{2}}[/tex]
Điều kiện cần: m-2>0 <=>m>2
Điều kiện đủ: [tex]\sqrt{\frac{m-2}{2}}\neq \sqrt{m}[/tex] (luôn thỏa mãn với m>2)
Vậy điều kiện cần tìm là m>2.
Đặc điểm của hàm |f(x)| là: |f(x)|=f(x) khi [TEX]f(x) \geq 0[/TEX]
và |f(x)|= - f(x) khi [TEX]f(x)<0[/TEX]
Do đó phần đồ thị của f(x) nằm bên dưới Ox thì sẽ lấy đối xứng lên trên qua trục đối xứng là Ox.
Một phần nằm bên dưới Ox của đường thẳng y=x:
Khi lấy đối xứng lên qua trục Ox:
Do vậy, ta có 1 số kết luận sau:
+ Các cực trị của hàm f(x) cũng vẫn là cực trị của hàm |f(x)|
+ Các nghiệm bội lẻ của f(x) là cực trị của |f(x)| . ( thực ra nghiệm bội chẵn vẫn là cực trị thôi, nhưng nó cũng chính là cưc trị của f(x), nên khi đếm vào thì ta có thể đếm trùng )
=> Tổng số cực trị của hàm |f(x)| là số cực trị của f(x)+ số nghiệm bội lẻ của f(x).
Ví dụ : Số cực trị của hàm [tex]f(x)=|x^3-3x^2-9x|[/tex]
Xét hàm: [TEX]y=x^3-3x^2-9x[/TEX], [TEX]y'=3x^2-6x-9[/TEX]
[TEX]y'=0<=>x=-1; x=3[/TEX]
Vậy hàm y có 2 cực trị.
Sử dụng casio bấm nghiệm pt : [TEX]y=x^3-3x^2-9x[/TEX] có 3 nghiệm: [TEX]x=0;x=-1,85;x=4,85[/TEX]
=> Hàm f(x) có số cực trị là 3+2=5
Mô phỏng đồ thị của hàm:
Vận dụng: Tìm giá trị của m để hàm số : [tex]f(x)=|x^4-x^3-5x^2+m|[/tex] có 7 điểm cực trị
Xét hàm [TEX]g(x)=x^4-x^3-5x^2+m[/TEX], ta có : [TEX]g'(x)=4x^3-3x^2-10x[/TEX]
[TEX]g'(x)=0<=>x=0,x=2,x=-5/4[/TEX]
Vậy hàm số f(x) có 3 điểm CT cũng là 3 điểm CT của g(x). Vậy để hàm f(x) có 7 điểm CT thì pt g(x)=0 có 4 nghiệm phân biệt.
Ta có: [TEX]g(x)=0<=>-x^4+x^3+5x^2=m[/TEX]
Xét hàm [TEX]v(x)=-x^4+x^3+5x^2[/TEX] , ta có BBT của hàm như sau:
Dựa vào BBT, ta thấy đường y=m cắt đồ thị v(x) tại 4 điểm phân biệt ( hay pt có 4 nghiệm phân biệt ) khi :
[TEX]0<m<\frac{875}{256}[/TEX]
Vận dụng 2: Tìm điều kiện của m để hàm số : [TEX]f(x)=(x^2+2)|x^2-m|[/TEX] có đúng 5 điểm cực trị
Đưa [TEX]x^2+2[/TEX] vào trong trị tuyệt đối ta có [TEX]f(x)=|(x^2+2)(x^2-m)|[/TEX]
Xét hàm g(x)=[TEX](x^2+2)(x^2-m)[/TEX] là hàm bậc 4, nên chỉ có tối đa 3 CT.
pt [TEX]g(x)=0[/TEX] chỉ có thể có nghiệm [TEX]x^2=m[/TEX]
Vậy nếu [TEX]m \leq 0[/TEX] thì pt g(x)=0 có tối đa 1 nghiệm => Có tối đa 4 CT, không thỏa mãn.
Vậy m>0 là điều kiện cần, khi đó g(x)=0 có 2 nghiệm : [tex]x=\sqrt{m},x=-\sqrt{m}[/tex]
Điều kiện đủ :
g(x) có 3 điểm CT khác với nghiệm của g(x)=0 :
[TEX]g(x)=x^4-(m-2)x^2-2m[/TEX], [TEX]g'(x)=4x^3-2(m-2)x[/TEX]
[TEX]g'(x)=0<=>x=0,[/TEX][tex]x=\sqrt{\frac{m-2}{2}},x=-\sqrt{\frac{m-2}{2}}[/tex]
Điều kiện cần: m-2>0 <=>m>2
Điều kiện đủ: [tex]\sqrt{\frac{m-2}{2}}\neq \sqrt{m}[/tex] (luôn thỏa mãn với m>2)
Vậy điều kiện cần tìm là m>2.
