[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
mn giúp mik 2 câu này vs
Vật lí 12 con lắc đơn
- Thread starter leduymanh2005
- Ngày gửi
- Replies 1
- Views 314
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Hocmai Forum 
leduymanh2005
[imath]1/[/imath]
[imath]2/[/imath]
Gọi [imath]a_1,a_2,g_1,g_2[/imath] lần lượt là gia tốc do lực điện trường gây ra và gia tốc trọng trường biểu kiến của hai con lắc [imath]1[/imath] và [imath]2[/imath]
Chúc bạn học tốt!
-----
Xem thêm: Tóm tắt tổng hợp kiến thức vật lí 12
[imath]1/[/imath]
| [imath]a/[/imath] Gia tốc lớn nhất tại biên âm suy ra [imath]x_1=-A=-10cm[/imath] Đi từ [imath]x_1[/imath] đến [imath]x_7[/imath] hết nửa chu kì, tức là quay được nửa vòng, vậy suy ra [imath]x_7[/imath] là biên dương. Hay [imath]x_7=A=10cm[/imath] Vì đi qua các li độ trong các khoảng thời gian bằng nhau [imath]\Delta t[/imath] nên điểm pha trên đường tròn cũng cách đều nhau. Từ đường tròn suy ra mỗi cung liên tiếp có giá trị là [imath]\dfrac{\pi}{6} \ rad[/imath] - Khoảng cách nhỏ nhất giữa hai điểm gần nhau liên tiếp tương ứng điểm pha [imath]P_1,P_2[/imath] hoặc [imath]P_6,P_7[/imath] [imath]L=A-\dfrac{A\sqrt{3}}{2}\approx 1,4 cm[/imath] - Khoảng cách lớn nhất giữa hai điểm gần nhau liên tiếp tương ứng điểm pha [imath]P_3,P_4[/imath] hoặc [imath]P_4,P_5[/imath] [imath]L'=\dfrac{A}{2}=5cm[/imath] [imath]b/[/imath] Tần số góc: [imath]\omega = \dfrac{\dfrac{\pi}{6}}{0,1}=\dfrac{5\pi}{3}[/imath] Trong thời gian [imath]0,8s[/imath], điểm pha quét được góc là: [imath]\Delta \varphi = \dfrac{5\pi}{3}.0,8 = \dfrac{4\pi}{3}=\pi+\dfrac{\pi}{3} \ rad[/imath] Khi góc quét được là [imath]\pi[/imath] thì quãng đường tương ứng là [imath]2A=20cm[/imath] Để tốc độ trung bình lớn nhất thì cung [imath]\dfrac{\pi}{3}[/imath] phải đối xứng nhau qua trục tung (trục vận tốc), quãng đường sẽ lớn nhất và bằng [imath]s=2.\dfrac{A}{2}=10cm[/imath] Tốc độ trung bình lớn nhất trong [imath]0,8s[/imath]: [imath]v=\dfrac{2A+s}{0,8}=\dfrac{20+10}{0,8}=37,5cm[/imath] |  |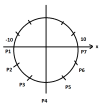
[imath]2/[/imath]
Gọi [imath]a_1,a_2,g_1,g_2[/imath] lần lượt là gia tốc do lực điện trường gây ra và gia tốc trọng trường biểu kiến của hai con lắc [imath]1[/imath] và [imath]2[/imath]
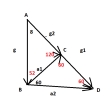
| Vì hai con lắc cùng đặt trong một điện trường đều nên: [imath]a_1=a_2=\dfrac{|q|E}{m}[/imath] [imath]T_2 > T_1[/imath] nên [imath]g_2 < g_1[/imath] như hình vẽ Tam giác [imath]BCD[/imath] có [imath]BC=BD[/imath] [imath](a_1=a_2)[/imath] và có góc [imath]60^{\circ}[/imath] suy ra tam giác này đều. Từ đây giải ra các góc màu đỏ như trong hình Định lí hàm số [imath]\sin[/imath] trong tam giác [imath]ABC[/imath]: [imath]\dfrac{g}{\sin120}=\dfrac{g_2}{\sin 52} (1)[/imath] Định lí hàm số [imath]\sin[/imath] trong tam giác [imath]ABD[/imath]: [imath]\dfrac{g}{\sin60}=\dfrac{g_1}{\sin (52+60)} (2)[/imath] Từ [imath](1),(2)[/imath] suy ra [imath]\dfrac{g_1}{g_2} \approx 1,18[/imath] Mặt khác: [imath]T_1=2\pi\sqrt{\dfrac{l}{g_1}}[/imath] [imath]T_2=2\pi\sqrt{\dfrac{l}{g_2}}[/imath] [imath]\Rightarrow \dfrac{T_1}{T_2}=\sqrt{\dfrac{1}{1,18}}[/imath] Lại có [imath]T_2 = T_1 + 0,1s[/imath] tìm được [imath]T_2=1,259s[/imath] |  |
Chúc bạn học tốt!
-----
Xem thêm: Tóm tắt tổng hợp kiến thức vật lí 12