[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
| - Thiết lập biểu thức lực căng khi ở vị trí [imath]\alpha[/imath] bất kì: Con lắc đơn dao động điều hòa được thì góc [imath]\alpha[/imath] phải nhỏ Khi đó [imath]\sin \alpha \approx \alpha ; \cos\alpha \approx 1-\dfrac{\alpha ^2}{2}[/imath] Xét vật tại vị trí li độ góc [imath]\alpha[/imath] như hình Theo phương hướng tâm ta có: [imath]T-mg\cos \alpha = m.\dfrac{v^2}{L}[/imath] ([imath]L[/imath] là chiều dài dây treo) [imath]\hArr T-mg(1-\dfrac{\alpha ^2}{2})=m.\dfrac{v^2}{L} \ (1)[/imath] Chọn gốc thế năng tại vị trí thấp nhất Bảo toàn cơ năng tại vị trí [imath]\alpha[/imath] và vị trí [imath]\alpha _m[/imath] [imath]\dfrac{1}{2}mv^2+mgL(1-\cos\alpha )=mgL(1-\cos \alpha _m) \Leftrightarrow \dfrac{1}{2}mv^2+mgL.\dfrac{\alpha ^2}{2}=mgL.\dfrac{\alpha _m^2}{2}\Leftrightarrow v^2=gL(\alpha _m^2 - \alpha ^2) \ (2)[/imath] Thay [imath](2)[/imath] vào [imath](1)[/imath] biến đổi ta được: [imath]T=mg(\alpha _m^2-\dfrac{3}{2}\alpha ^2 +1)[/imath] - Từ biểu thức trên, để [imath]T=T_{max}[/imath] thì góc [imath]\alpha _{min}[/imath] suy ra [imath]\alpha = 0[/imath] Hay: Vật ở vị trí cân bằng thì lực căng cực đại - Tính độ lớn lực căng cực đại khi [imath]\alpha _m = 60^{\circ}[/imath]: Biểu thức lực căng cực đại [imath]T_{max}=mg.(\alpha_m^2 +1) = 2.10.((\dfrac{\pi}{3})^2+1) \approx 41,93N[/imath] |  [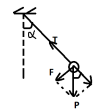imath]F[/imath] trên hình là lực hồi phục nhé. |
Hocmai Forum 