K
kuteme011
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
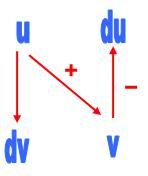
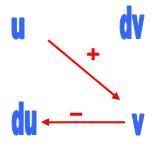
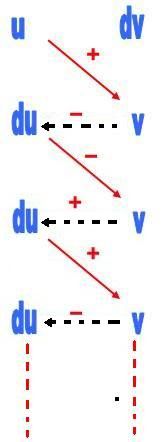
[TEX]\int_{}^{}(x^3-4x^2+2x+3)sinxdx[/TEX]
các bạn thử giải xem và đừng nên tách ra và sử dụng từng phần vì tôi tin chắc ko ai đủ kiên nhẫn làm vậy đâu? hãy làm cách khác hay hơn nhé! chúc may mắn
nếu lâu wé mà ko ai giải thì tôi sẽ đưa câu trả lời lên sau )(khoảng hơn 1 tuần)
)(khoảng hơn 1 tuần)
các bạn thử giải xem và đừng nên tách ra và sử dụng từng phần vì tôi tin chắc ko ai đủ kiên nhẫn làm vậy đâu? hãy làm cách khác hay hơn nhé! chúc may mắn
nếu lâu wé mà ko ai giải thì tôi sẽ đưa câu trả lời lên sau
kimxakiem2507:
[TEX]*[/TEX] Đây là bài tích phân toàn phần quá cơ bản mà em, tách ghép làm gì cho mệt,cứ để im đó mà làm!
Last edited by a moderator: