View attachment 200758 Cho △ABC có ma, mb, mc lần lượt là độ dài đường trung tuyến của tam giác xuất phát từ đỉnh A,B,C. Đặt m=(ma+mb+mc)/2. CMR diện tích △ABC đc tính theo công thức:
S=4/3 căn m(m-ma)(m-mb)(m-mc)
Giúp mình nhé. Mình cảm ơn mọi người nhiều ạ.
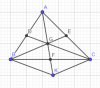
Gọi $D,E,F$ lần lượt là trung điểm của $AB,AC,BC$
$G$ là trọng tam giác $ABC$
Gọi $K$ là điểm đối xứng của $A$ qua $G$
Ta có: $\dfrac{GF}{AG}=\dfrac12\Rightarrow \dfrac{GF}{GK}=\dfrac12$
$\Rightarrow F$ là trung điểm của $BC$
Mà $F$ là trung điểm của $BC$
Suy ra $BGCK$ là hình bình hành
$BG=\dfrac{2}{3}m_b; GK=\dfrac{2}{3}m_a; BK=\dfrac{2}{3}m_c$
Ta có CT: $S=\sqrt{p(p-a)(p-b)(p-c)}$
nên $S_{BGK}=\dfrac{4}{9}\sqrt{m(m-m_a)(m-m_b)(m-m_c)}$
$S_{ABC}=2 S_{ABF}=6 S_{BGF}=3S_{BGK}=\dfrac43 \sqrt{m(m-m_a)(m-m_b)(m-m_c)}$
Có gì khúc mắc em hỏi lại nhé
Ngoài ra em có thể tham khảo thêm các kiến thức tại:
https://diendan.hocmai.vn/threads/t...o-ban-hoan-toan-mien-phi.827998/#post-4045397
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Cho △ABC có ma, mb, mc lần lượt là độ dài đường trung tuyến của tam giác xuất phát từ đỉnh A,B,C. Đặt m=(ma+mb+mc)/2. CMR diện tích △ABC đc tính theo công thức:
