[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
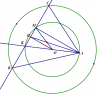
Cho 2 đường tròn đồng tâm O bán kính $R$ và $r$ $( R>r)$ .Gọi $M,A$ là 2 điểm trên đường tròn $(O;r)$ với $M$ cố định và $A$ chuyển động. Qua $M$ vẽ dây $BC$ của $(O;R)$ vuông góc $AM$. Gọi $H$ là hình chiếu của $O$ trên $BC.CM$.
a) $AM=2.OH$
b) $MA^2+MB^2+MC^2$ ko đổi
c)Trọng tâm tam giác $ABC$ cố định
Mọi người giúp em với ạ tks.


a) $AM=2.OH$
b) $MA^2+MB^2+MC^2$ ko đổi
c)Trọng tâm tam giác $ABC$ cố định
Mọi người giúp em với ạ tks.